polux@huggy$ tom TermList.t && javac TermList.java && java TermList
Original subject
 |
Insertion with term-graph rules from Gom
 |
Tom ManualEmilie Balland, |
Tom is a software environment for defining transformations. It is built as a language extension which adds new matching primitives to C, Java, and Caml.
In Java for example, the integration is smooth, allowing the use of the Java Runtime Library without any restriction.
The main construct of Tom is %match, which is similar to the match primitive found in functional languages: given an object (called subject) and a list of patterns-actions, the match primitive selects the first pattern that matches the subject and performs the associated action. The subject against which we match can be any object, but in practice, this object is usually a tree-based data-structure.
The %match construct can be seen as an extension of the classical switch/case construct. The main difference is that the discrimination occurs on a term and not on atomic values like characters or integers: the patterns are used to discriminate and retrieve information from an algebraic data structure. Therefore, Tom is a good language for programming by pattern matching, and it is particularly well-suited for programming various transformations on trees/terms or Xml data-structures.
Information on Tom is available at tom.loria.fr.
Writing a good documentation is a difficult task. To help new users,
as well as confirmed Tom developers, we have split the documentation
into four complementary documents:
Here you can find the detailed table of contents:
Part I |
We provide here cut and paste examples, each of them illustrates one particular aspect of the Tom language. Every code snippet comes with the command line to compile and execute it along with the associated program output.
polux@huggy$ tom Algebraic.t && javac Algebraic.java && java Algebraic
implies(P(plus(nat(1),nat(2))),Q(var("x")))
true
polux@huggy$ tom Matching.t && javac Matching.java && java Matching I was here ! (P(1 + 2) => Q(x))
polux@huggy$ tom Anti.t && javac Anti.java && java Anti - Not a car, or car with different colors: bike() - Not a car, or car with different colors: car(red(),green(),ecological()) - Ecological car and that has the same interior and exterior colors, but different from green: car(red(),red(),ecological()) - Not a car, or car with different colors: car(green(),red(),polluting()) - Car that is not ecological and that does not have the same interior and exterior colors: car(green(),red(),polluting())
polux@huggy$ tom RmDoubles.t && javac RmDoubles.java && java RmDoubles
strlist("framboisier","eric","framboisier","remi","remi","framboisier","rene","bernard")
strlist("framboisier","eric","remi","rene","bernard")
polux@huggy$ tom Eval.t && javac Eval.java && java Eval
plus(val(2),var("x"),mult(val(3),val(4)),var("y"),val(5))
plus(var("x"),var("y"),val(19))
polux@huggy$ tom Collect.t && javac Collect.java && java Collect
vars: [var("x"), var("y")]
polux@huggy$ tom Advanced.t && javac Advanced.java && java Advanced free occurences of x: [] free occurences of y: [[2, 1, 2, 1], [2, 2, 1, 1]]
polux@huggy$ tom Sort.t && javac Sort.java && java Sort sorted(1,3,5,7,9) sorted(0,2,4,6,8) sorted(0,1,2,3,4,5,6,7,8,9,10)
polux@huggy$ tom Sort.t && javac Sort.java && java Sort 3 is greater than the head of sorted(9) 5 is greater than the head of sorted(3,9) 5 is greater than the head of sorted(9) 7 is greater than the head of sorted(3,5,9) 7 is greater than the head of sorted(5,9) 7 is greater than the head of sorted(9) sorted(1,3,5,7,9)
polux@huggy$ tom Mapping.t && javac Mapping.java && java Mapping list = [1, 2, 3, 1, 4, 3, 1, 1] iterate: 1 iterate: 2 iterate: 3 iterate: 1 iterate: 4 iterate: 3 iterate: 1 iterate: 1 appears twice: 1 appears twice: 1 appears twice: 1 appears twice: 3 appears twice: 1 appears twice: 1 appears twice: 1 appears only once: 2 appears only once: 4
polux@huggy$ tom HandMapping.t && javac HandMapping.java && java HandMapping this red car has 6 seats c1 and c3 have the same blue color This is the same blue car with 4 seats
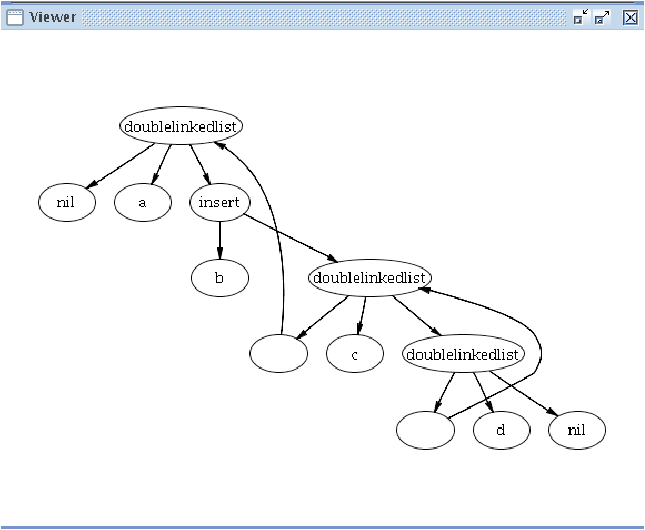
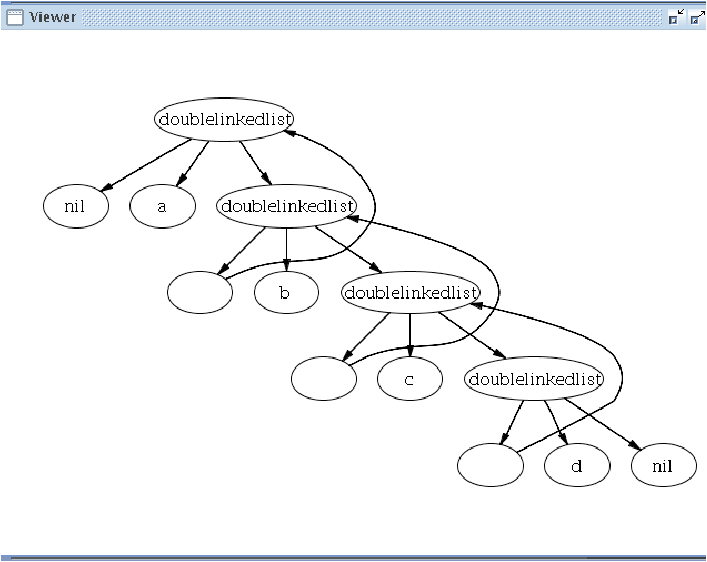
Using the Gom option --termgraph, it is possible to automatically generate from a signature the extended version for term-graphs. As the Tom terms are implemented with maximal sharing, so are the term-graphs. Term-graphs can be specified using label constructors.
Users can define a system of term-graph rules and it is automatically compiled in a basic Tom strategy. These term-graph rewriting rules can then be integrated in a more complex strategy using Tom strategy combinators. As a consequence, all Tom features are available for term-graphs.
polux@huggy$ tom TermList.t && javac TermList.java && java TermList
Original subject
 |
Insertion with term-graph rules from Gom
 |
This formalism is presented in http://hal.inria.fr/inria-00173535/fr.
Part II |
In the following we consider that the reader is familiar with the Java programming language. Since a potential Tom user may have a background very different from another one, we sometimes address a particular topic which may appear too technical or too theoretical. We use (*) and (**) to indicate such sections that may be omitted in the first reading.
Tom is an extension of Java that can be considered as a preprocessor. Therefore, any Java construct can be used in a Tom program. The tom command line compiler takes a Tom file, whose extension should be .t, and generates a Java file with the extension .java. The Java compiler (javac) has to be used to produce the class file.
In this first part, we introduce the basic notions provided by Tom: the definition of a data-type, the construction of data (i.e. trees), and the transformation of such data using pattern-matching.
One of the most simple Tom programs is the following. It defines a data-type to represent Peano integers and builds the integers 0=zero and 1=suc(zero):
import main.peano.types.*;
public class Main {
%gom {
module Peano
abstract syntax
Nat = zero()
| suc(pred:Nat)
| plus(x1:Nat, x2:Nat)
}
public final static void main(String[] args) {
Nat z = `zero();
Nat one = `suc(z);
System.out.println(z);
System.out.println(one);
}
}
The %gom{ …} constructs defines a data-structure, also called signature or algebraic data-type. This data-structure declares a sort (Nat) that has three operators (zero, suc, and plus). These operators are called constructors, because they are used to construct the data-structure. zero is a constant (arity 0), whereas the arity of suc and plus is respectively 1 and 2. Note that a name has to be given for each slot (pred for suc, and x1, x2 for plus).
A second construct provided by Tom is the ‘ (backquote), which builds an object. The expression ‘zero() builds the object zero of sort Nat. This is equivalent to new zero().
In the example, the variable z is a Java object that can be used in ‘suc(z) to build the object suc(zero()). In other words, an algebraic data-structure definition can be seen as a grammar. The ‘ construct allows to build trees (Abstract Syntax Trees) over this grammar.
The implementation generated by Gom is such that objects can be converted into readable strings, using the toString() method.
In the following we assume that Tom is installed, as explained in chapter 14. To run the example, do a copy and paste into Main.t, then compile the file using the command: tom Main.t. Then, compile the generated Java file: javac Main.java, and run it with java Main, as shown below:
$ tom Main.t $ javac Main.java $ java Main zero() suc(zero())
The path corresponds to the name of the class (Main), followed by the name of the module (Peano), followed by types.*. These package names are in lowercase, even if the class name and the module name contain capitals.
In addition to %gom and ‘, Tom provides a third construct: %match. Using the same program, we add a method evaluate(Nat n) and we modify the method run():
import main.peano.types.*;
public class Main {
%gom {
module Peano
abstract syntax
Nat = zero()
| suc(pred:Nat)
| plus(x1:Nat, x2:Nat)
}
public final static void main(String[] args) {
Nat two = `plus(suc(zero()),suc(zero()));
System.out.println(two);
two = evaluate(two);
System.out.println(two);
}
public static Nat evaluate(Nat n) {
%match(n) {
plus(x, zero()) -> { return `x; }
plus(x, suc(y)) -> { return `suc(plus(x,y)); }
}
return n;
}
}
The %match construct is similar to switch/case in the sense that given a tree (n), the %match selects the first pattern that matches the tree, and executes the associated action. By matching, we mean: giving values to variables to make the pattern equal to the subject. In our example n has the value plus(suc(zero()),suc(zero())). The first pattern does not match n, because the second subterm of n is not a zero(), but a suc(zero()). In this example, the second pattern matches n and gives the value suc(zero()) to x, and zero() to y.
When a pattern matches a subject, we say that the variables (x and y in our case) are instantiated. They can then be used in the action part (also called right-hand side). Similarly, the second rules can be applied when the second subterm is rooted by a suc. In that case, x and y are instantiated.
The method evaluate defines the addition of two integers represented by Peano successors (i.e. zero and suc). The first case says that the addition of an integer with zero is evaluated into the integer itself. The second case builds a new term (rooted by suc) whose subterm (plus(x,y)) denotes the addition of x and y.
When executing the program we obtain:
plus(suc(zero()),suc(zero())) suc(plus(suc(zero()),zero()))
In this section, we will show how to use the notion of rules to simplify expressions. Suppose that we want to simplify boolean expressions. It is frequent to define the relations between expressions using a set of simplification rules like the following:
|
To encode such a simplification system, we have to implement a function that simplifies an expression until no more reduction can be performed. This can of course be done using functions defined in Java, combined with the %match constructs, but it is more convenient to use an algebraic construct that ensures that a rule is applied whenever a reduction is possible. For this purpose, the %gom construct provides a rule() construct where the left and the right-hand sides are terms. The previous simplification system can be defined as follows:
import gates.logic.types.*;
public class Gates {
%gom {
module Logic
imports int
abstract syntax
Bool = Input(n:int)
| True()
| False()
| Not(b:Bool)
| Or(b1:Bool, b2:Bool)
| And(b1:Bool, b2:Bool)
| Nand(b1:Bool, b2:Bool)
| Xor(b1:Bool, b2:Bool)
module Logic:rules() {
Not(a) -> Nand(a,a)
Or(a,b) -> Nand(Not(a),Not(b))
And(a,b) -> Not(Nand(a,b))
Xor(a,b) -> Or(And(a,Not(b)),And(Not(a),b))
Nand(False(),_) -> True()
Nand(_,False()) -> True()
Nand(True(),True()) -> False()
}
}
public final static void main(String[] args) {
Bool b = `Xor(True(),False());
System.out.println("b = " + b);
}
}
When using the module Logic:rules() { ... } constructs, the simplification rules are integrated into the data-structure. This means that the rules are applied any time it is possible to do a reduction. The user does not have any control on them, and thus cannot prevent from applying a rule. Of course, the simplification system should be terminating, otherwise, infinite reductions may occur. When compiling and executing the previous program, we obtain b = True().
When programming large applications, it may be more convenient to introduce several classes that share a common data-structure. In that case, the %gom {...} construct could be avoided and a Gom file (Logic.gom for example) could be used instead:
module Logic
imports int
abstract syntax
Bool = Input(n:int)
| True()
| False()
| Not(b:Bool)
| Or(b1:Bool, b2:Bool)
| And(b1:Bool, b2:Bool)
| Nand(b1:Bool, b2:Bool)
| Xor(b1:Bool, b2:Bool)
module Logic:rules() {
Not(a) -> Nand(a,a)
Or(a,b) -> Nand(Not(a),Not(b))
And(a,b) -> Not(Nand(a,b))
Xor(a,b) -> Or(And(a,Not(b)),And(Not(a),b))
Nand(False(),_) -> True()
Nand(_,False()) -> True()
Nand(True(),True()) -> False()
}
This file can by compiled as follows:
$ gom Logic.gom
This generates several Java classes, among them a particular file called Logic.tom which explains to Tom how the data-structure is implemented. This process is hidden when using the %gom {...} construct:
$ ls logic _Logic.tom Logic.tom LogicAbstractType.java strategy types
One of the simplest Tom program that uses the defined data-structure is the following:
import logic.types.*;
public class Main {
%include{ logic/Logic.tom }
public final static void main(String[] args) {
Bool b = `Xor(True(),False());
System.out.println("b = " + b);
}
}
In the Tom program, %include { logic/Logic.tom } is necessary to include (like a copy and paste) the Logic.tom file generated by gom. The %include command is similar to the #include command provided by the C-preprocessor.
In this section we present how Tom can be used to describe the abstract syntax and to implement an interpreter for a given language. We also give some tips and more information about the generated code.
When using %gom { ... }, the generated data-structure is particular: data are maximally shared. This technique, also known as hash-consing ensures that two identical subterms are implemented by the same objects. Therefore, the memory footprint is minimal and the equality-check can be done in constant time using the == construct (two terms are identical if the pointers are equal). As a consequence, a term is not mutable: once created, it cannot be modified.
Even if the generated API offers getters and setters for each defined slot (Bool getb1(), Bool getb2(), Bool setb1(Bool t) and Bool setb2(Bool t) for the And(b1:Bool,b2:Bool) defined below). These methods do not really modify the term on which they are applied: t.setb1(‘True()) will return a copy of t where the first child is set to True(), but the previous t is not modified. There is no side-effect in a maximally shared setting.
In Tom, it is quite easy to quickly develop applications which manipulates trees. As an example, let us consider a tiny language composed of boolean expressions (True, False, And, Or, and Not), expressions (constant, variable, Plus, Mult, and Mod), and instructions (Skip, Print, ;, If, and While). The abstract syntax of this language can be described as follows:
import pico1.term.types.*;
import java.util.*;
class Pico1 {
%gom {
module Term
imports int String
abstract syntax
Bool = True()
| False()
| Not(b:Bool)
| Or(b1:Bool, b2:Bool)
| And(b1:Bool, b2:Bool)
| Eq(e1:Expr, e2:Expr)
Expr = Var(name:String)
| Cst(val:int)
| Plus(e1:Expr, e2:Expr)
| Mult(e1:Expr, e2:Expr)
| Mod(e1:Expr, e2:Expr)
Inst = Skip()
| Assign(name:String, e:Expr)
| Seq(i1:Inst, i2:Inst)
| If(cond:Bool, i1:Inst, i2:Inst)
| While(cond:Bool, i:Inst)
| Print(e:Expr)
}
...
}
Assume that we want to write an interpreter for this language, we need a notion of environment to store the value assigned to a variable. A simple solution is to use a Map which associate an expression (of sort Expr) to a name of variable (of sort String). Given this environment, the evaluation of an expression can be implemented as follows:
public static Expr evalExpr(Map env,Expr expr) {
%match(expr) {
Var(n) -> { return (Expr)env.get(`n); }
Plus(Cst(v1),Cst(v2)) -> { return `Cst(v1 + v2); }
Mult(Cst(v1),Cst(v2)) -> { return `Cst(v1 * v2); }
Mod(Cst(v1),Cst(v2)) -> { return `Cst(v1 % v2); }
// congruence rules
Plus(e1,e2) -> { return `evalExpr(env,Plus(evalExpr(env,e1),evalExpr(env,e2))); }
Mult(e1,e2) -> { return `evalExpr(env,Mult(evalExpr(env,e1),evalExpr(env,e2))); }
Mod(e1,e2) -> { return `evalExpr(env,Mod(evalExpr(env,e1),evalExpr(env,e2))); }
x -> { return `x; }
}
throw new RuntimeException("should not be there: " + expr);
}
We will see later how they can be avoided using the notion of strategy.
Similarly, the evaluation of boolean expressions can be implemented as follows:
public static Bool evalBool(Map env,Bool bool) {
%match(bool) {
Not(True()) -> { return `False(); }
Not(False()) -> { return `True(); }
Not(b) -> { return `evalBool(env,Not(evalBool(env,b))); }
Or(True(),_) -> { return `True(); }
Or(_,True()) -> { return `True(); }
Or(False(),b2) -> { return `b2; }
Or(b1,False()) -> { return `b1; }
And(True(),b2) -> { return `b2; }
And(b1,True()) -> { return `b1; }
And(False(),_) -> { return `False(); }
And(_,False()) -> { return `False(); }
Eq(e1,e2) -> {
Expr x = `evalExpr(env,e1);
Expr y = `evalExpr(env,e2);
return (x==y)?`True():`False();
}
x -> { return `x; }
}
throw new RuntimeException("should not be there: " + bool);
}
Once defined the methods evalExpr and evalBool, it becomes easy to define the interpreter:
public static void eval(Map env, Inst inst) {
%match(inst) {
Skip() -> {
return;
}
Assign(name,e) -> {
env.put(`name,evalExpr(env,`e));
return;
}
Seq(i1,i2) -> {
eval(env,`i1);
eval(env,`i2);
return;
}
Print(e) -> {
System.out.println(evalExpr(env,`e));
return;
}
If(b,i1,i2) -> {
if(evalBool(env,`b)==`True()) {
eval(env,`i1);
} else {
eval(env,`i2);
}
return;
}
w@While(b,i) -> {
Bool cond = evalBool(env,`b);
if(cond==`True()) {
eval(env,`i);
eval(env,`w);
}
return;
}
}
throw new RuntimeException("strange term: " + inst);
}
Note also the use of w@... that introduces a variable w (an alias). This variable can be used in the action part to avoid building the term While(b,i).
To play with the Pico language, we just have to initialize the environment (env), create programs (p1 and p2), and evaluate them (eval):
public final static void main(String[] args) {
Map env = new HashMap();
Inst p1 = `Seq(Assign("a",Cst(1)) , Print(Var("a")));
System.out.println("p1: " + p1);
eval(env,p1);
Inst p2 = `Seq(Assign("i",Cst(0)),
While(Not(Eq(Var("i"),Cst(10))),
Seq(Print(Var("i")),
Assign("i",Plus(Var("i"),Cst(1))))));
System.out.println("p2: " + p2);
eval(env,p2);
}
A very simple program is the following:
public class HelloWorld {
%include { string.tom }
public final static void main(String[] args) {
String who = "World";
%match(who) {
"World" -> { System.out.println("Hello " + who); }
_ -> { System.out.println("Don't panic"); }
}
}
}
The %include { string.tom } construct imports the predefined (Java) mapping which defines the Tom String algebraic sort. Thus, the sort String can be used in the %match construct.
This examples shows that pattern matching can be performed against built-in data-types. In this example, the %match construct is equivalent to a switch/case construct: as expected the first print statement is executed, but the second one is also executed since no break statement has been executed.
To use a break statement in a %match construct, we recommend to use the notion of labeled block:
public class HelloWorld {
%include { string.tom }
public final static void main(String[] args) {
String who = "World";
matchblock: {
%match(who) {
"World" -> { System.out.println("Hello " + who);
break matchblock;
}
_ -> { System.out.println("Don't panic"); }
}
}
}
}
One particularity of Tom is to simplify the manipulation of lists.
It is natural to consider a string as a list of characters. Characters can be concatenated to from a string, and string can also be concatenated. In Tom, we have to give a name to this concatenation operator. Let us call it concString.
Thus, the string “Hello” is equivalent to the list of characters concString(’H’,’e’,’l’,’l’,’o’).
Given a string, to check if the string contains the character ‘e’, we can use the following matching construct:
public class HelloWorld {
%include { string.tom }
public final static void main(String[] args) {
%match("Hello") {
concString(_*,'e',_*) -> { System.out.println("we have found a 'e'"); }
}
}
}
In this example, ‘_*’ corresponds to an anonymous variable which can be instantiated by any list of characters (possibly reduced to the empty list).
In order to capture the context (i.e. what is before and after the ‘e’), it is possible to use named variables:
%match(t) {
concString(before*,'e',after*) -> {
System.out.println("we have found a 'e'" +
" after " + `before* +
" but before " + `after*);
}
}
In this example, we have introduced two new variables (before* and after*), called “variable-star”, which are instantiated by a list of characters, instead of a single character (if the ‘*’ was not there).
Suppose now that we look for a word whose last letter is a ‘o’:
%match(t) {
concString(before*,'o') -> { ... }
}
Using this mechanism, it also becomes possible to look for a word which contains an ‘e’ somewhere and an ‘o’ in last position:
%match(t) {
concString(before*,'e',_*,'o') -> { ... }
}
Note that a single pattern could provide several outcomes:
%match(t) {
concString(before*,'l',after*) -> {
System.out.println("we have found " + `before* +
" before 'l' and " + `after* + " after");
}
}
When applied to “Hello”, there are two possible solutions for before* and after*:
we have found he before 'l' and lo after we have found hel before 'l' and o after
Let us suppose that we look for two consecutive ‘l’ anywhere in the matched expression. This could be expressed by:
%match(t) {
concString(_*,'l','l',_*) -> { ... }
}
Since this syntax is error prone when looking for long/complex substrings, Tom provides an abbreviated notation: ‘ll’:
%match(t) {
concString(_*,'ll',_*) -> { ... }
}
This notation is fully equivalent to the previous one.
In the following, we consider the program:
public class StringMatching {
%include { string.tom }
public final static void main(String[] args) {
String s = "abcabc";
%match(s) {
concString(_*,x,_*,x,_*) -> { System.out.println("x = " + `x); }
concString('a',_*,y,_*,'c') -> { System.out.println("y = " + `y); }
concString(C1*,'abc',C2*) -> { System.out.println("C1 = " + `C1*); }
concString(_*,z@'bc',_*) -> { System.out.println("z = " + `z); }
concString(_*,L*,_*,L*,_*) -> { if(`L*.length() > 0) {
System.out.println("L = " + `L*); } }
}
}
As illustrated previously, we can use variables to capture contexts. In fact, this mechanism is more general and we can use a variable anywhere to match something which is not statically known. The following pattern looks for two characters which are identical:
concString(_*,x,_*,x,_*) -> { System.out.println("x = " + `x); }
Since list matching is not unitary, there may be several results. In this case, we obtain:
x = a x = b x = c
The second pattern looks for a character in a string which should begin with a ‘a’ and end with a ‘c’:
concString('a',_*,y,_*,'c') -> { System.out.println("y = " + `y); }
The results are:
y = b y = c y = a y = b
The third pattern look for the substring ‘abc’ anywhere in the string:
concString(C1*,'abc',C2*) -> { System.out.println("C1 = " + `C1*); }
When the substring is found, the prefix C1* is:
C1 = C1 = abc
The last pattern illustrates the search of two identical substrings:
concString(_*,L*,_*,L*,_*) -> { if(`L*.length() > 0) {
System.out.println("L = " + `L*); } }
The results are:
L = a L = ab L = abc L = b L = bc L = c
To look for a palindrome, you can use the following pattern:
%match(t) {
concString(x*,y*,y*,x*) -> { /* we have found a palindrome */ }
}
As illustrated previously, Tom supports a generalized form of string matching, called list matching, also known as associative matching with neutral element. In Tom, some operators are special and do not have a fixed number of arguments. This intuitively corresponds to the idea of list where elements are stored in a given order. A list of elements may be written (a,b,c) or [a,b,c]. In Tom, it is written f(a(),b(),c()), where ‘f’ is this special operator. In some sense, ‘f’ is the name of the list. This allows to distinguish list of apples, from list of oranges for examples.
The definition of such operators can be done using Gom:
import list1.list.types.*;
public class List1 {
%gom {
module List
abstract syntax
E = a()
| b()
| c()
L = f( E* )
}
...
}
Once this signature defined, it becomes possible to define patterns and ‘ expressions. For example, the function that removes identical consecutive elements can be expressed as follows:
public static L removeDouble(L l) {
%match(l) {
f(X1*,x,x,X2*) -> {
return removeDouble(`f(X1*,x,X2*));
}
}
return l;
}
This example is interesting since it expresses a complex operation in a concise way: given a list l, the %match construct looks for two identical consecutive elements (f(X1*,x,x,X2*) is called a non-linear pattern since x appears twice). If there exists such two elements, the term f(X1*,x,X2*) is built (an x has been removed), and the removeDouble function is called recursively. When there is no such two elements, the pattern does not match, this means that the list does not contain any consecutive identical elements. Therefore, the instruction return l is executed and the function returns.
Similarly, a sorting algorithm can be implemented: if a list contains two elements in the wrong order, just swap them. This can be expressed as follows:
public static L swapSort(L l) {
%match(l) {
f(X*,e1,Z*,e2,Y*) -> {
if(`gt(e1,e2)) {
return `swapSort(f(X*,e2,Z*,e1,Y*));
}
}
}
return l;
}
private static boolean gt(E e1, E e2) {
return e1.toString().compareTo(e2.toString()) > 0;
}
In this example, the order is implemented by the gt function, using the lexicographical ordering provided by Java.
1. X*=f(), e1=b(), Z*=f(), e2=b(), Y*=f(a(),a()) 2. X*=f(), e1=b(), Z*=f(b()), e2=a(), Y*=f(a()) 3. X*=f(), e1=b(), Z*=f(b(),a()), e2=a(), Y*=f() 4. X*=f(b()), e1=b(), Z*=f(), e2=a(), Y*=f(a) 5. X*=f(b()), e1=b(), Z*=f(a()), e2=a(), Y*=f() 6. X*=f(b(),b()), e1=a, Z*=f(), e2=a(), Y*=f()Assuming that a < b, there are only 4 solutions (2, 3, 4, and 5 since e1 must be greater than e2) that can be used to apply the rule
It becomes important to remind you how a rule is applied in Tom:
Let us suppose that Tom computes the solution 1. first (the order in which solutions are computed is not fixed and depends on the implementation). In that case, the test if(‘gt(e1,e2)) is evaluated. Since b() is not greater than b(), the return swapSort(...) is not performed.
As specified in Section 10.2.2, another solution is computed. Let us say 2.. In that case, the test becomes true and the function swapSort is called recursively.
The following code shows how to build a list and call the function defined previously. This results in sorted lists where elements only occur once.
public final static void main(String[] args) {
L l = `f(a(),b(),c(),a(),b(),c(),a());
L res1 = swapSort(l);
L res2 = removeDouble(res1);
System.out.println(" l = " + l);
System.out.println("sorted l = " + res1);
System.out.println("single l = " + res2);
}
We call strategy an elementary transformation. Suppose that you want to transform the object a() into the object b(). You can of course use all the functionalities provided by Tom and Java. But in that case, you will certainly end in mixing the transformation (the piece of code that really replaces a() by b()) with the control (the Java part that is executed in order to perform the transformation).
The notion of strategy is a clear separation between control and transformation. In our case, we will define a strategy named Trans1 that only describes the transformation we have in mind:
import main.example.types.*;
import tom.library.sl.*;
public class Main {
%gom {
module Example
abstract syntax
Term = a() | b() | f(x:Term)
}
%include { sl.tom }
public final static void main(String[] args) {
try {
Term t1 = `a();
Term t2 = (Term) `Trans1().visit(t1);
System.out.println("t2 = " + t2);
} catch(VisitFailure e) {
System.out.println("the strategy failed");
}
}
%strategy Trans1() extends Fail() {
visit Term {
a() -> b()
}
}
}
There exists three kinds of elementary strategy: Fail, which always fails, Identity, which always succeeds, and transformation rules of the form l → r.
(a -> b)[a] = b (a -> b)[b] = failure (a -> b)[f(a)] = failure (Identity)[a] = a (Identity)[b] = b (Identity)[f(a)] = f(a) (Fail)[a] = failure
The sequential operator, Sequence(S1,S2), applies the strategy S1, and then the strategy S2. It fails if either S1 fails, or S2 fails.
(Sequence(a -> b, b -> c))[a] = c (Sequence(a -> b, c -> d))[a] = failure (Sequence(b -> c, a -> b))[a] = failure
The choice operator, Choice(S1,S2), applies the strategy S1. If the application S1 fails, it applies the strategy S2. Therefore, Choice(S1,S2) fails if both S1 and S2 fail.
(Choice(a -> b, b -> c))[a] = b (Choice(b -> c, a -> b))[a] = b (Choice(b -> c, c -> d))[a] = failure (Choice(b -> c, Identity))[a] = a
The strategy Not(S), applies the strategy and fails when S succeeds. Otherwise, it succeeds and corresponds to the Identity.
(Not(a -> b))[a] = failure (Not(b -> c))[a] = a
By combining basic combinators, more complex strategies can be defined. To make the definitions generic, parameters can be used. For example, we can define the two following strategies:
(Try(b -> c))[a] = a (Repeat(a -> b))[a] = b (Repeat(Choice(b -> c, a -> b)))[a] = c (Repeat(b -> c))[a] = a
We consider two kinds of traversal strategy (All(S) and One(S)). The first one applies S to all subterms, whereas the second one applies S to only one subterm.
The application of the strategy All(S) to a term t applies S on each immediate subterm of t. The strategy All(S) fails if S fails on at least one immediate subterm.
(All(a -> b))[f(a)] = f(b) (All(a -> b))[g(a,a)] = g(b,b) (All(a -> b))[g(a,b)] = failure (All(a -> b))[a] = a (All(Try(a -> b)))[g(a,c)] = g(b,c)
The application of the strategy One(S) to a term t tries to apply S on an immediate subterm of t. The strategy One(S) succeeds if there is a subterm such that S can be applied. The subterms are tried from left to right.
(One(a -> b))[f(a)] = f(b) (One(a -> b))[g(a,a)] = g(b,a) (One(a -> b))[g(b,a)] = g(b,b) (One(a -> b))[a] = failure
By combining the previously mentioned constructs, it becomes possible to define well know strategies:
BottomUp(S) = Sequence(All(BottomUp(S)), S) TopDown(S) = Sequence(S, All(TopDown(S))) OnceBottomUp(S) = Choice(One(OnceBottomUp(S)), S) OnceTopDown(S) = Choice(S, One(OnceTopDown(S))) Innermost(S) = Repeat(OnceBottomUp(S)) Outermost(S) = Repeat(OnceTopDown(S))
Let us consider again a Pico language whose syntax is a bit simpler than the one seen in section 5.5.
import pico2.term.types.*;
import java.util.*;
import tom.library.sl.*;
class Pico2 {
%include { sl.tom }
%gom {
module Term
imports int String
abstract syntax
Bool = True()
| False()
| Neg(b:Bool)
| Or(b1:Bool, b2:Bool)
| And(b1:Bool, b2:Bool)
| Eq(e1:Expr, e2:Expr)
Expr = Var(name:String)
| Cst(val:int)
| Let(name:String, e:Expr, body:Expr)
| Seq( Expr* )
| If(cond:Bool, e1:Expr, e2:Expr)
| Print(e:Expr)
| Plus(e1:Expr, e2:Expr)
}
...
}
As an exercise, we want to write an optimization function that replaces an instruction of the form If(Neg(b),i1,i2) by a simpler one: If(b,i2,i1). A possible implementation is:
public static Expr opti(Expr expr) {
%match(expr) {
If(Neg(b),i1,i2) -> { return `opti(If(b,i2,i1)); }
x -> { return `x; }
}
throw new RuntimeException("strange term: " + expr);
}
public final static void main(String[] args) {
Expr p4 = `Let("i",Cst(0),
If(Neg(Eq(Var("i"),Cst(10))),
Seq(Print(Var("i")), Let("i",Plus(Var("i"),Cst(1)),Var("i"))),
Seq()));
System.out.println("p4 = " + p4);
System.out.println("opti(p4) = " + opti(p4));
}
When executing this program, we obtain:
p4 = Let("i",Cst(0),If(Neg(Eq(Var("i"),Cst(10))),
ConsSeq(Print(Var("i")),ConsSeq(Let("i",
Plus(Var("i"),Cst(1)),Var("i")),EmptySeq)),EmptySeq))
opti(p4) = Let("i",Cst(0),If(Neg(Eq(Var("i"),Cst(10))),
ConsSeq(Print(Var("i")),ConsSeq(Let("i",
Plus(Var("i"),Cst(1)),Var("i")),EmptySeq)),EmptySeq))
This does not correspond to the expected result, simply because the opti function performs an optimization when the expression starts with an If instruction. To get the expected behavior, we have to add congruence rules that will allow to apply the rule in subterms (one rule for each constructor):
public static Expr opti(Expr expr) {
%match(expr) {
If(Neg(b),i1,i2) -> { return `opti(If(b,i2,i1)); }
// congruence rules
Let(n,e1,e2) -> { return `Let(n,opti(e1),opti(e2)); }
Seq(head,tail*) -> { return `Seq(opti(head),opti(tail*)); }
If(b,i1,i2) -> { return `If(b,opti(i1),opti(i2)); }
Print(e) -> { return `Print(e); }
Plus(e1,e2) -> { return `Plus(e1,e2); }
x -> { return `x; }
}
throw new RuntimeException("strange term: " + expr);
}
Since this is not very convenient, we will show how the use of strategies can simplify this task.
Let us start with a very simple task which consists in printing all the nodes that corresponds to a constant (Cst(_). To do that, we have to define an elementary strategy that is successful when it is applied on a node Cst(_):
%strategy stratPrintCst() extends Fail() {
visit Expr {
Cst(x) -> { System.out.println("cst: " + `x); }
}
}
To traverse the program and print all Cst nodes, a TopDown strategy can be applied:
public static void printCst(Expr expr) {
try {
`TopDown(Try(stratPrintCst())).visit(expr);
} catch (VisitFailure e) {
System.out.println("strategy failed");
}
}
public final static void main(String[] args) {
...
System.out.println("p4 = " + p4);
printCst(p4);
}
This results in:
p4 = Let("i",Cst(0),If(Neg(Eq(Var("i"),Cst(10))),
ConsSeq(Print(Var("i")),ConsSeq(Let("i",
Plus(Var("i"),Cst(1)),Var("i")),EmptySeq)),EmptySeq))
cst: 0
cst: 10
cst: 1
As a second exercise, we will try to write another strategy that performs the same task, but we will try to separate the strategy that looks for a constant from the strategy that prints a node. So, let us define these two strategies:
%strategy FindCst() extends Fail() {
visit Expr {
c@Cst(x) -> c
}
}
%strategy PrintTree() extends Identity() {
visit Expr {
x -> { System.out.println(`x); }
}
}
Similarly to stratPrintCst, the strategy FindCst extends Fail. The goal of the PrintTree strategy is to print a node of sort Expr. By extending Identity, we specify the default behavior when the strategy is applied on a term of a different sort.
To print the node Cst, we have to look for a Cst and print this node. This can be done by combining, using a Sequence, the two strategies FindCst and PrintTree:
public static void printCst(Expr expr) {
try {
`TopDown(Try(stratPrintCst())).visit(expr);
`TopDown(Try(Sequence(FindCst(),PrintTree()))).visit(expr);
} catch (VisitFailure e) {
System.out.println("strategy failed");
}
}
This results in:
cst: 0 cst: 10 cst: 1 Cst(0) Cst(10) Cst(1)
Here, we will try to rename all the variables from a given program: the name should be modified into _name.
To achieve this task, you can define a primitive strategy that performs the modification, and apply it using a strategy such as TopDown:
%strategy stratRenameVar() extends Fail() {
visit Expr {
Var(name) -> { return `Var("_"+name); }
}
}
public static void optimize(Expr expr) {
try {
`Sequence(TopDown(Try(stratRenameVar())),PrintTree()).visit(expr);
} catch (VisitFailure e) {
System.out.println("strategy failed");
}
}
The application of optimize to p4 results in:
Let("i",Cst(0),If(Neg(Eq(Var("_i"),Cst(10))),
ConsSeq(Print(Var("_i")),ConsSeq(Let("i",
Plus(Var("_i"),Cst(1)),Var("_i")),EmptySeq)),EmptySeq))
Suppose now that we want to print the intermediate steps: we do not want to perform all the replacements in one step, but for debugging purpose, we want to print the intermediate term after each application of the renaming rule.
The solution consists in combining the stratRenameVar strategy with the PrintTree strategy.
A first solution consists in applying stratRenameVar using a OnceBottomUp strategy, and immediately apply PrintTree on the resulting term. This could be implemented as follows:
`Repeat(Sequence(OnceBottomUp(stratRenameVar()),PrintTree())).visit(expr);
Unfortunately, this results in:
Let("i",Cst(0),If(Neg(Eq(Var("_i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("__i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("___i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("____i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("_____i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("______i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("_______i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("________i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("_________i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("__________i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("___________i"),Cst(10))),...
Let("i",Cst(0),If(Neg(Eq(Var("____________i"),Cst(10))),...
...
This is not the expected behavior! Why?
Simply because the renaming rule can be applied several times on a same variable. To fix this problem, we have to apply the renaming rule only if the considered variable has not already be renamed.
To know if a variable has been renamed, you just have to define an elementary strategy, called RenamedVar, that succeeds when the name of the variable starts with an underscore. This can be easily implemented using string matching capabilities:
%strategy RenamedVar() extends Fail() {
visit Expr {
v@Var(('_',name*)) -> v
}
}
To finish our implementation, it is sufficient to apply stratRenameVar only when RenamedVar fails, i.e., when Not(RenamedVar) succeeds.
`Repeat(Sequence(
OnceBottomUp(Sequence(Not(RenamedVar()),stratRenameVar())),
PrintTree())
).visit(expr);
This results in (layouts have been added to improve readability):
Let("i",Cst(0),If(Neg(Eq(Var("_i"),Cst(10))),
ConsSeq(Print(Var("i")),ConsSeq(Let("i",
Plus(Var("i"),Cst(1)),Var("i")),EmptySeq)),EmptySeq))
Let("i",Cst(0),If(Neg(Eq(Var("_i"),Cst(10))),
ConsSeq(Print(Var("_i")),ConsSeq(Let("i",
Plus(Var("i"),Cst(1)),Var("i")),EmptySeq)),EmptySeq))
Let("i",Cst(0),If(Neg(Eq(Var("_i"),Cst(10))),
ConsSeq(Print(Var("_i")),ConsSeq(Let("i",
Plus(Var("_i"),Cst(1)),Var("i")),EmptySeq)),EmptySeq))
Let("i",Cst(0),If(Neg(Eq(Var("_i"),Cst(10))),
ConsSeq(Print(Var("_i")),ConsSeq(Let("i",
Plus(Var("_i"),Cst(1)),Var("_i")),EmptySeq)),EmptySeq))
Now that you know how to use strategies, it should be easy to implement the tiny optimizer seen in the beginning of section 7.2.
You just have to define the transformation rule and a strategy that will apply the rule in an innermost way:
%strategy OptIf() extends Fail() {
visit Expr {
If(Neg(b),i1,i2) -> If(b,i2,i1)
}
}
public void optimize(Expr expr) {
try {
`Sequence(Innermost(OptIf()),PrintTree()).visit(expr);
} catch (VisitFailure e) {
System.out.println("strategy failed");
}
}
Applied to the program p4, as expected this results in:
Let("i",Cst(0),If(Eq(Var("i"),Cst(10)),EmptySeq,
ConsSeq(Print(Var("i")),ConsSeq(Let("i",
Plus(Var("i"),Cst(1)),Var("i")),EmptySeq))))
Tom patterns support the use of complements, called anti-patterns. In other words, it is possible to specify what you don’t want to match. This is done via the ‘!’ symbol, according to the grammar defined in the language reference.
If we consider the Gom signature
import list1.list.types.*;
public class List1 {
%gom {
module List
abstract syntax
E = a()
| b()
| c()
| f(x1:E, x2:E)
| g(x3:E)
L = List( E* )
}
...
}
a very simple use of the anti-patterns would be
...
%match(subject) {
!a() -> {
System.out.println("The subject is different from 'a'");
}
}
...
The ‘!’ symbols can be nested, and therefore more complicated examples can be generated:
...
%match(subject) {
f(a(),!b()) -> {
// matches an f which has x1=a() and x2!=b()
}
f(!a(),!b()) -> {
// matches an f which has x1!=a() and x2!=b()
}
!f(a(),!b()) -> {
// matches either something different from f(a(),_) or f(a(),b())
}
!f(x,x) -> {
// matches either something different from f, or an f with x1 != x2
}
f(x,!x) -> {
// matches an f which has x1 != x2
}
f(x,!g(x)) -> {
// matches an f which has either x2!=g or x2=g(y) with y != x1
}
}
...
The anti-patterns can be also quite useful when used with lists. Imagine that you what to search for a list that doesn’t contain a specific element. Without the use of anti-patterns, you would be forced to match with a variable instead of the element you don’t want, and after that to perform a test in the action part to check the contents of the variable. For the signature defined above, if we are looking for a list that doesn’t contain a(), using the anti-patterns we would write:
...
%match(listSubject) {
!List(_*,a(),_*) -> {
System.out.println("The list doesn't contain 'a'");
}
}
...
Please note that this is different from writing
...
%match(listSubject) {
List(_*,!a(),_*) -> {
// at least an element different from a()
}
}
...
which would match a list that has at least one element different from a().
Some more useful anti-patterns can be imagined in the case of lists:
...
%match(listSubject) {
!List(_*,!a(),_*) -> {
// matches a list that contains only 'a()'
}
!List(X*,X*) -> {
// matches a non-symmetrical list
}
!List(_*,x,_*,x,_*) -> {
// matches a list that has all the elements distinct
}
List(_*,x,_*,!x,_*) -> {
// matches a list that has at least two elements that are distinct
}
}
...
Since version 2.6 of the language, a more modular syntax for %match and %strategy is proposed. Instead of having a pattern (or several for more subjects) as the left-hand side of rules in a %match or %strategy, now more complex conditions can be used.
Let’s consider the following class that includes a Gom signature:
import constraints.example.types.*
public class Constraints {
%gom {
module Example
abstract syntax
E = a()
| b()
| c()
| f(x1:E, x2:E)
| g(x3:E)
L = List( E* )
}
...
}
Let’s now suppose that we have the following %match construct:
...
%match(subject) {
f(x,y) -> {
boolean flag = false;
%match(y){
g(a()) -> { flag = true; }
f(a(),b()) -> { flag = true; }
}
if (flag) { /* some action */ }
}
g(_) -> { System.out.println("a g(_)"); }
}
...
This is a very basic example where we want to check if the subject is an f with the second sub-term either g(a()) or f(a(),b()). If it is the case, we want to perform an action.
Using the new syntax of the %match construct (detailed in the language reference), we could write the following equivalent code:
...
%match(subject) {
f(x,y) && ( g(a()) << y || f(a(),b()) << y ) -> { /* some action */ }
g(_) -> { System.out.println("g()"); }
}
...
The %match construct can be also used without any parameters. The following three constructs are all equivalent:
...
%match(subject1, subject2) {
p1,p2 -> { /* action 1 */ }
p3,p4 -> { /* action 2 */ }
}
...
...
%match(subject1) {
p1 && p2 << subject2 -> { /* action 1 */ }
p3 && p4 << subject2 -> { /* action 2 */ }
}
...
...
%match {
p1 << subject1 && p2 << subject2 -> { /* action 1 */ }
p3 << subject1 && p4 << subject2 -> { /* action 2 */ }
}
...
A big advantage of the this approach compared to the classical one is its flexibility. The right-hand side of a match constraint can be a term built on variables coming from the left-hand sides of other constraints, as we saw in the first example of this section. A more advanced example could verify for instance that a list only contains two occurrences of an object:
...
%match(sList) {
List(X*,a(),Y*,a(),Z*) && !List(_*,a(),_*) << List(X*,Y*,Z*) -> {
System.out.println("Only two objects a()");
}
}
...
In the above example, the first pattern checks that the subject contains two objects a(), and the second constraint verifies that the rest of the list doesn’t contain any a().
Besides match constraints introduced with the symbol <<, we ca also have boolean constraints by using the following operators: >, >=, <, <=, == and !=. These can be used between any terms, and are trivially translated into host code (this means that the constraint term1 == term2 will correspond exactly to an if (term1 == term2) ... in the generated code). A simple example is the following one, which prints all the elements in a list of integers that are bigger than 5:
...
%gom {
module Example
imports int
abstract syntax
Lst = intList( int* )
}
Lst sList = `intList(6,7,4,5,3,2,8,9);
%match(sList) {
intList(_*,x,_*) && x > 5 -> { System.out.println(`x);
}
}
...
...
%strategy MyStrat() extends Identity() {
visit E {
f(x,y) && ( g(a()) << y || f(a(),b()) << y ) -> { /* some action */ }
}
}
...
This is particulary useful even for simple conjunctions, as in a %strategy we cannot have multiple subjects like in %match.
...
%match {
x << a() || x << b() -> { System.out.println("here x=" + `x); }
}
...
Up to now, we have considered examples where the implementation of data-types is either predefined (Xml case), or generated by a tool (Gom case). One interesting contribution of Tom is to be customizable. By defining a mapping between the signature formalism (%typeterm, %op, etc.) and the concrete implementation, it becomes possible to perform pattern matching against any data-structure.
In this section, we consider that we have a Java library for representing tree based data structures. On another side, to be able to use Tom, we consider the following abstract data-type:
%typeterm Nat %op Nat zero() %op Nat suc(Nat)
By doing so, we have defined a sort (Nat), and two operators (zero and suc). When defining a mapping, the goal consists in explaining to Tom how the considered abstract data-type is implemented, and how a term (over this signature) can be de-constructed.
For expository reasons, the ATerm library is the Java library used to implement terms. However, any other tree/term based library could have been used instead.
In order to define a correct mapping, we have to describe how the algebraic sort (Nat in our example) is implemented (by the ATermAppl class). This is done via the implement construct:
%typeterm Nat {
implement { ATermAppl }
}
The second part of the mapping definition consists in defining how the symbols (zero and suc) are represented in memory. This is done via the is_fsym construct:
%op Nat zero() {
is_fsym(t) { t.getName().equals("zero") }
}
%op Nat suc(pred:Nat) {
is_fsym(t) { t.getName().equals("suc") }
get_slot(pred,t) { (ATermAppl)t.getArgument(0) }
}
In addition, get_slot describes how to retrieve a subterm of a term.
Given a term built over the ATerm library, it becomes possible to perform pattern matching as previously explained.
When using the backquote construct (‘suc(suc(zero)) for example), Tom has to know how to build a term in memory. For this purpose, we consider an extension of the signature definition formalism: the make construct.
%op Nat zero() {
is_fsym(t) { t.getName().equals("zero") }
make { SingletonFactory.getInstance().makeAppl(
SingletonFactory.getInstance().makeAFun("zero",0,false)) }
}
%op Nat suc(pred:Nat) {
is_fsym(t) { t.getName().equals("suc") }
get_slot(pred,t) { (ATermAppl)t.getArgument(0) }
make(t) { SingletonFactory.getInstance().makeAppl(
SingletonFactory.getInstance().makeAFun("suc",1,false),t) }
}
The makeAFun function has three arguments: the function name, the number of arguments and a boolean that indicates if the quotes are included in the function name or not.
Given this mapping, Tom can be used as previously: the following function implements the addition of two Peano integers:
public ATermAppl plus(ATermAppl t1, ATermAppl t2) {
%match(t2) {
zero() -> { return t1; }
suc(y) -> { return `suc(plus(t1,y)); }
}
return null;
}
Let us suppose that we have a Java class Person with two getters (getFirstname and getLastname). In order to illustrate the signature definition formalism, we try to redefine (without using Gom) the abstract data type for the sort Person.
The first thing to do consists in defining the Tom sort Person:
%typeterm Person {
implement { Person }
}
To avoid any confusion, we use the same name twice: the Tom sort Person is implemented by the Java class Person. When declaring an operator, we defined the behavior as shown in the previous example:
%op Person person(firstname:String, lastname:String) {
is_fsym(t) { t instanceof Person }
get_slot(firstname,t) { t.getFirstname() }
get_slot(lastname,t) { t.getLastname() }
make(t0, t1) { new Person(t0, t1) }
}
In this example, we illustrate another possibility offered by Tom: being able to know whether a term is rooted by a symbol without explicitly representing this symbol. The is_fsym(t) construct should return true when the term t is rooted by the algebraic operator we are currently defining. In this example, we say that the term t is rooted by the symbol person when the object t is implemented by an instance of the class Person. By doing so, we do not explicitly represent the symbol person, even if it could have been done via the reflective capabilities of Java (by using Person.getClass() for example).
In this section, we show how to describe a mapping for associative operators.
%typeterm TomList {
implement { ArrayList }
equals(l1,l2) { l1.equals(l2) }
}
Assuming that the sort Element is already defined, we can use the %oparray construct to define an associative operator. We also have to explain to Tom how to compute the size of a list, and how to access a given element. This is done via get_size and get_element constructs:
%oparray TomList conc( Element* ) {
is_fsym(t) { t instanceof ArrayList }
get_element(l,n) { (ATermAppl)l.get(n) }
get_size(l) { l.size() }
make_empty(n) { myEmpty(n) }
make_append(e,l) { myAdd(e,(ArrayList)l) }
}
This construct is similar to %op except that additional information have to be given: how to build an empty list (make_empty), and how to add an element to a given list (make_append). The auxiliary Java functions are defined as follows:
private static ArrayList myAdd(Object e,ArrayList l) {
l.add(e);
return l;
}
private static ArrayList myEmpty(int n) {
ArrayList res = new ArrayList(n);
return res;
}
Usually, we use an associative operator to represent (in a abstract way) a list data structure. There are many ways to implement a list, but the two most well-known are the use of array based list, and the use of linked-list. The previously described mapping shows how to map an abstract list to an array based implementation.
Tom offers another similar construct %oplist to map an associative operator to a linked-list based implementation. When using the ATerm library for example, a possible implementation could be:
%typeterm TomTerm {
implement { aterm.ATermAppl }
equals(t1, t2) { t1==t2 }
}
%typeterm TomList {
implement { ATermList }
equals(l1,l2) { l1==l2 }
}
%oplist TomList conc( TomTerm* ) {
is_fsym(t) { t instanceof aterm.ATermList }
make_empty() { aterm.pure.SingletonFactory.getInstance().makeList() }
make_insert(e,l) { l.insert(e) }
get_head(l) { (aterm.ATermAppl)l.getFirst() }
get_tail(l) { l.getNext() }
is_empty(l) { l.isEmpty() }
}
Even if this section mostly deals with Xml features, every explained technique can be used with other data-structures as well.
This example is inspired from a practical study. It involves a simple modeling of the Platform for Privacy Preferences Project (P3P), developed by the World Wide Web Consortium, which is emerging as an industry standard providing a simple, automated way for users to gain more control over the use of personal information on Web sites they visit.
Given a client and a server, the problem consists in verifying that the client’s policy is compliant with the server’s policy. Both policies preferences are expressed in APPEL (A P3P Preference Exchange Language) and written in Xml. The server’s policy is the following file server.xml:
<POLICIES xmlns="http://www.w3.org/2002/01/P3Pv1">
<POLICY name="mypolicy" discuri="http://www.ibm.com/privacy"
opturi="http://www.ibm.com/privacy" xml:lang="en">
<STATEMENT>
<RECIPIENT> <delivery/> </RECIPIENT>
<PURPOSE> <contact/> </PURPOSE>
<DATA-GROUP>
<DATA ref="#dynamic.clickstream"/>
<DATA ref="#dynamic.http"/>
<DATA ref="#dynamic.clientevents"/>
<DATA ref="#user.home-info.postal.country"/>
<DATA ref="#dynamic.cookies"> <CATEGORIES> <content/> </CATEGORIES> </DATA>
</DATA-GROUP>
</STATEMENT>
</POLICY>
</POLICIES>
The client’s policy is the following file client.xml:
<RULESET appel="http://www.w3.org/2002/04/APPELv1"
p3p="http://www.w3.org/2000/12/P3Pv1"
crtdby="W3C" crtdon="2001-02-19T16:21:21+01:00">
...
<RULE behavior="limited1" prompt="yes">
<POLICY>
<STATEMENT>
<PURPOSE connective="and-exact"> <current/> </PURPOSE>
<RECIPIENT connective="or">
<other-recipient/>
<public/>
<unrelated/>
</RECIPIENT>
</STATEMENT>
</POLICY>
</RULE>
...
<RULE behavior="request" prompt="yes">
<POLICY>
<STATEMENT>
<DATA-GROUP>
<DATA ref="#dynamic.clientevents"> </DATA>
<DATA ref="#dynamic.clickstream"/>
</DATA-GROUP>
</STATEMENT>
</POLICY>
</RULE>
...
</RULESET>
For expository reasons, we consider only a sub-problem in which we say that a client’s policy is compatible with the server’s policy if all ref attributes from a <DATA></DATA> node also appear on the server side. In the considered examples, the policies are compatible because
<DATA-GROUP> <DATA ref="#dynamic.clientevents"> </DATA> <DATA ref="#dynamic.clickstream"/> </DATA-GROUP>
is included in:
<DATA-GROUP> <DATA ref="#dynamic.clickstream"/> <DATA ref="#dynamic.http"/> <DATA ref="#dynamic.clientevents"/> <DATA ref="#user.home-info.postal.country"/> <DATA ref="#dynamic.cookies"> <CATEGORIES> <content/> </CATEGORIES> </DATA> </DATA-GROUP>
The problem consists in implementing such a verification tool in Tom and Java.
The first part of the program declares imports, and defines the main and the run methods.
import tom.library.xml.*;
import tom.library.adt.tnode.*;
import tom.library.adt.tnode.types.*;
import aterm.*;
import java.util.*;
public class Evaluator {
%include{ adt/tnode/TNode.tom }
private XmlTools xtools;
public static void main (String args[]) {
xtools = new XmlTools();
TNode server = (TNode)xtools.convertXMLToATerm("server.xml");
TNode client = (TNode)xtools.convertXMLToATerm("client.xml");
boolean compatible = compareDataGroup(getDataGroup(server.getDocElem()),
getDataGroup(client.getDocElem()));
System.out.println("result = " + compatible);
}
...
}
As explained in Part III (Tom language description), to each Xml document corresponds a DOM (Document Object Model) representation. In Tom, we have defined a mapping from DOM sorts to abstract algebraic sorts: TNode and TNodeList, which correspond respectively to Node and NodeList, defined by the Java DOM implementation.
This mapping has to be initialized in the following way:
In complement to Tom, we provide a runtime library which contains several methods to manipulate Xml documents. In particular, we provide the XmlTools class (defined in the tom.library.xml.* package).
The run method takes two filenames as arguments, reads the associated files and convert their Xml content into TNode terms (using the convertXMLToATerm function).
The getDataGroup function is used to retrieve a <DATA></DATA> node in the considered Xml document. Note that getDocElem is first applied to Xml documents in order to consider subterms of the DocumentNode element. Then, the compareDataGroup function is used to check that the client’s policy is compatible with the server’s policy. The content of these functions is detailed in the next sections.
Given an Xml subtree, the problem consists in extracting a <DATA-GROUP></DATA-GROUP> node. For expository reasons, we first consider that such a <DATA-GROUP></DATA-GROUP> node can only appear at two different specific places: one for the client’s definition and one for the server’s definition.
Thus, in the Tom program we naturally consider two cases:
private static TNode getDataGroup(TNode doc) {
%match(doc) {
<POLICIES>
<POLICY>
<STATEMENT>
datagroup@<DATA-GROUP></DATA-GROUP>
</STATEMENT>
</POLICY>
</POLICIES> -> { return datagroup; }
<RULESET>
<RULE>
<POLICY>
<STATEMENT>
datagroup@<DATA-GROUP></DATA-GROUP>
</STATEMENT>
</POLICY>
</RULE>
</RULESET> -> { return datagroup; }
}
return `xml(<DATA-GROUP/>);
}
The first pattern means that a <DATA-GROUP></DATA-GROUP> node has to be found under a <STATEMENT></STATEMENT> node, which should be under a <POLICY></POLICY> node, which should be under a <POLICIES></POLICIES> node. Once such a pattern is found, the mechanism allows us to give a name (datagroup) to this subterm and reuse it in the action part: return datagroup;.
The Xml notation implicitly extends the given patterns by adding context variables. Thus, the <DATA-GROUP></DATA-GROUP> pattern means that a subterm those head symbol is <DATA-GROUP></DATA-GROUP> is searched. But this subterm can contain attributes and children even if it is not explicitly defined by the notation. To make the definition of patterns more precise, the user can use the explicit notation and define the following pattern: <DATA-GROUP (_*)>(_*)</DATA-GROUP>. A more detailed explanation can be found in Part III (Tom language description).
Given two <DATA-GROUP></DATA-GROUP> nodes, the problem consists in checking that all <DATA></DATA> nodes from the first tree also appear in the second one. This can be easily implemented by the following couple of functions:
private static boolean compareDataGroup(TNode server, TNode client) {
boolean res = true;
%match(client) {
<DATA-GROUP><DATA ref=reftext></DATA></DATA-GROUP>
-> { res = res && appearsIn(reftext,server); }
}
return res;
}
Given a <DATA-GROUP></DATA-GROUP> tree, we look for a <DATA></DATA> subtree which contains an attribute named ref. When such an attribute exists, its content (a string) is stored into the Java reftext variable. The appearsIn function is then used to check that the attribute also appears on the server side.
private static boolean appearsIn(String refclient, TNode server) {
%match(server) {
<DATA-GROUP><DATA ref=reftext></DATA></DATA-GROUP>
-> {
if(reftext.equals(refclient)) {
return true;
}
}
}
return false;
}
This piece of code is interesting because it introduces what we call "conditional rules". Given the string refclient we look for a <DATA></DATA> subtree containing a ref attribute with exactly the same string. Since it is not possible to use an instantiated variable in a pattern (something like <DATA ref=refclient>...</DATA>, we have to introduce a fresh variable reftext and check in a condition that this variable is equal to refclient. This is done via a Java condition (the if clause): the action part (return true;) is executed only when the condition is satisfied, and clearly it will end the method. If the condition is not satisfied, then the next <DATA></DATA> subtree is searched. It is exactly the case of a switch statement, when the action part is not exited by a return, break or goto, and the control flow is transferred to the next matching solution or the next matching pattern.
If no such subtree exists, this means that the two policies are not compatible and false is returned.
The Tom runtime library provides a set of generic functions in order to perform various kinds of traversal over a term. This is useful when searching a pattern somewhere in a term, at any position. As the Xml documents are seen by Tom as terms, the different traversals on terms are also valid when dealing with Xml.
In the current example, the getDataGroup functions looks for a <DATA-GROUP></DATA-GROUP> node. Instead of statically specifying the path (POLICIES, POLICY, STATEMENT, DATA-GROUP and RULESET, RULE, POLICY, STATEMENT, DATA-GROUP) we could have used the generic traversal mechanism provided by the package tom.library.traversal.*.
private static GenericTraversal traversal = new GenericTraversal();
In the following, we generalize the previous problem by considering that we can have more than one appearance of the <DATA-GROUP></DATA-GROUP> node per Xml document.
We further expose the use of the generic traversal mechanism. The collectDatagroup method creates an inner class Collect1 with one method, apply, and then it calls the genericCollect method of the traversal object created previously with an object of this inner class as a parameter.
protected static void collectDatagroup(final Collection collection, TNode subject) {
Collect1 collect = new Collect1() {
public boolean apply(ATerm t) {
if(t instanceof TNode) {
%match(t) {
<DATA-GROUP> </DATA-GROUP> -> {
collection.add(t);
return false;
}
}
}
return true;
} // end apply
}; // end new
traversal.genericCollect(subject, collect);
}
Let us now analyze the inner class: firstly, it extends the class Collect1, where 1 stands for the number of arguments of the apply method, and secondly it implements the method apply. The method call traversal.genericCollect will call this method for all subtrees of the subject term. Since subject may contain subterms of different sorts (integers or strings for example), the instanceof construct is used as a first filter to select only the subterms which correspond to Xml nodes. When such a subterm is rooted by a <DATA-GROUP></DATA-GROUP>, the subterm is added to the collection (by a side-effect). The return false; statement indicates that it is no longer necessary to traverse the considered term (in our example, a <DATA-GROUP></DATA-GROUP> node cannot be found inside a <DATA-GROUP></DATA-GROUP> itself). Respectively, the return true; statement indicates that the apply function should be recursively applied to the current term in order to continue the traversal.
Given a collection, the getDataGroup method uses an iterator to select a <DATA-GROUP></DATA-GROUP> node.
private static TNode getDataGroup(TNode doc) {
HashSet c = new HashSet();
collectDatagroup(c,doc);
Iterator it = c.iterator();
while(it.hasNext()) {
TNode datagroup = (TNode)it.next();
return datagroup;
}
return `xml(<DATA-GROUP/>);
}
In this section, we consider a DOM mapping for Xml documents. This means that Xml documents are still considered as algebraic terms (built over TNode and TNodeList), but their internal representation is backed by the W3C DOM library.
In the following, we consider a small data-base represented by an Xml document person.xml:
<Persons> <Person Age="30"> <FirstName> Paul </FirstName> </Person> <Person Age="28"> <FirstName> Mark </FirstName> </Person> <Person Age="21"> <FirstName> Jurgen </FirstName> </Person> <Person Age="21"> <FirstName> Julien </FirstName> </Person> <Person Age="24"> <FirstName> Pierre-Etienne </FirstName> </Person> </Persons>
The problem consists in sorting this document according to different criteria (age or first-name for example).
The first part of the program declares imports, and defines the main method.
import org.w3c.dom.*;
import javax.xml.parsers.*;
import javax.xml.transform.*;
import javax.xml.transform.dom.DOMSource;
import javax.xml.transform.stream.StreamResult;
import java.io.File;
public class PersonSort1 {
private static Document dom;
%include{ dom.tom }
public static void main (String args[]) {
try {
dom = DocumentBuilderFactory.newInstance()
.newDocumentBuilder().parse("person.xml");
Element e = dom.getDocumentElement();
dom.replaceChild(sort(e),e);
Transformer transform = TransformerFactory.newInstance().newTransformer();
StreamResult result = new StreamResult(new File("Sorted.xml"));
transform.transform(new DOMSource(dom), result);
} catch (Exception e) {
e.printStackTrace();
}
}
...
}
The mapping has to be initialized in the following ways:
In order to implement a sorting algorithm, we need to know how to compare two elements.
The following function takes two Xml documents in argument and compares their attribute Age, using the string comparison operator compareTo.
private static int compare(Node t1, Node t2) {
%match(t1, t2) {
<Person Age=a1></Person>, <Person Age=a2></Person> -> {
return `a1.compareTo(`a2);
}
}
return 0;
}
In this example, it is interesting to note that an Xml node is seen as an associative operator. This feature, combined with the implicit notation, is such that <Person Age=a1></Person> will match any Xml node headed by Person which contains the attribute Age. This Xml node may contain several sub-nodes, but they will not be stored in any variable.
In this section we use a swap sort algorithm which consists in finding two elements that are not in the correct order. Once they are found, they are swapped before calling the algorithm recursively. When no two such elements exist, this means that the list is sorted.
private static Node sort(Node subject) {
%match(subject) {
<Persons>(X1*,p1,X2*,p2,X3*)</Persons> -> {
if(compare(`p1,`p2) > 0) {
return sort(`xml(dom,<Persons>X1* p2 X2* p1 X3*</Persons>));
}
}
}
return subject;
}
The pattern <Persons>(X1*,p1,X2*,p2,X3*)</Persons> looks for two elements p1 and p2 and stores the remaining contexts in X1*, X2*, and X3*. In order to give a name to contexts (and then retrieve them to build a new list), the pattern is written in explicit notation. This notation prevents Tom to add extra variables. Otherwise, the expanded form of <Persons>X1* p1 X2* p2 X3*</Persons> (written in explicit notation) would have been <Persons>(_*,X1*,_*,p1,_*,X2*,_*,p2,_*,X3*,_*)</Persons>.
Note that the action part is guarded by a condition (if(compare(p1,p2) > 0)). This means that return sort(...) is executed only when two bad-ordered elements are found. When p1 and p2 are correctly ordered, the matching procedure continues and extracts another couple p1 and p2. As mentioned in Part III, when Tom cannot find two elements p1 and p2 such that the condition is satisfied (the list is sorted), the return sort(...) statement is not executed and the control flow is transferred to the following statement: return subject;
As mentioned previously, when two elements have to be swapped, a new list is built. This done via the ‘‘’ (backquote) construct. This construct, used before to retrieve instantiated variables, can also be use to build a new term. In order to build an Xml document, the xml(...) function has to be used. The number of parameters depends on the Xml mapping which is used. In our case, when manipulating DOM objects, a new subtree is built is the context of a main document. This extra-parameter is given in the first argument of the xml function. Thus, ‘xml(dom,<Persons>...<Persons>) builds a new <Person></Person> node, as a child of the dom document. When using the TNode.tom mapping, a library based on Gom is used. In this case, it is no longer necessary (and even not correct) to use this extra argument.
In the previous section, we considered a sorting algorithm expressed in a pure functional programming style: when two elements have to be swapped, a new list is built and returned.
In the following example, we exploit OO-style of the DOM library and perform a swap in place: the list is updated by swapping two elements (with side effect):
private static void sort(Node subject) {
%match(subject) {
r @ <_>p1@<_ Age=a1></_> p2@<_ Age=a2></_></_> -> {
if(`a1.compareTo(`a2) > 0) {
`r.replaceChild(`p2.cloneNode(true),`p1);
`r.replaceChild(`p1,`p2);
`sort(r);
return;
}
}
}
}
In this example, we use the notion of anonymous Xml node (<_>...</_>) which allows to describe more generic algorithms.
Part III |
The syntax of the language is given in BNF-like notation. Terminal symbols are set in typewriter font (‘like this’). Non-terminal symbols are set in italic font (like that). Square brackets [...] denote optional components. Parentheses with a trailing star sign (...)* denotes zero, one or several repetitions of the enclosed components. Parentheses with a trailing plus sign (...)+ denote one or several repetitions of the enclosed components. Parentheses (...) denote grouping.
| Identifier | ::= | Letter ( Letter ∣ Digit ∣ ‘_’ ∣ ‘-’ )* |
| Integer | ::= | (Digit )+ |
| Double | ::= | (Digit)+ [‘.’] (Digit)* ∣ ‘.’ (Digit)+ |
| String | ::= | ‘"’ (Letter ∣ (‘\’ (‘n’ ∣ ‘t’ ∣ ‘b’ ∣ ‘r’ ∣ ‘f’ ∣ ‘\’ ∣ ‘’’ ∣ ‘"’) ) )* ‘"’ |
| Letter | ::= | ‘A’ ... ‘Z’ ∣ ‘a’ ... ‘z’ |
| Digit | ::= | ‘0’ ... ‘9’ |
| Char | ::= | ‘’’ (Letter ∣Digit) ‘’’ |
| SubjectName | ::= | Identifier |
| Type | ::= | Identifier |
| SlotName | ::= | Identifier |
| HeadSymbol | ::= | Identifier |
| ∣ | Integer | |
| ∣ | Double | |
| ∣ | String | |
| ∣ | Char | |
| VariableName | ::= | Identifier |
| AnnotedName | ::= | Identifier |
| LabelName | ::= | Identifier |
| FileName | ::= | Identifier |
| AttributeName | ::= | Identifier |
| XMLName | ::= | Identifier |
| Name | ::= | Identifier |
A Tom program is a host language program (namely C, Java, or Caml) extended by several new constructs such as %match, %strategy, %include, %gom, or backquote. Tom is a multi-language compiler, and therefore its syntax depends on the host language syntax. But for simplicity, we only present the syntax of its constructs and explain how they can be integrated into the host language.
Using Java as a host-language, the following Tom program is correct:
public class HelloWorld {
%include { string.tom }
public final static void main(String[] args) {
String who = "World";
%match(who) {
"World" -> { System.out.println("Hello " + who); }
_ -> { System.out.println("Don't panic"); }
}
}
}
A Tom program is a list of blocks, where each block is either a Tom construct, or a sequence of characters (host language code). When compiling a Tom program, the Tom constructs are transformed into host language code, and the result is a valid host language program. For instance, in the previous example, %include and %match constructs are replaced by function definitions and Java instructions, making the resulting program a correct Java program.
Syntax of a Tom program:
| Tom | ::= | BlockList |
| BlockList | ::= | |
| ( | MatchConstruct | |
| ∣ | StrategyConstruct | |
| ∣ | BackQuoteTerm | |
| ∣ | IncludeConstruct | |
| ∣ | GomConstruct | |
| ∣ | TypeTerm | |
| ∣ | Operator | |
| ∣ | OperatorList | |
| ∣ | OperatorArray | |
| ∣ | ‘{’ BlockList ‘}’ | |
| )* |
./packageName/, $TOM_HOME/share/jtom/ and <path>,
where <path> is specified by option: --import <path>.
If the file contains some Tom constructs, they are expanded.The %match construct (MatchConstruct) is one of the main contributions of Tom. This construct can be seen as an extension of the SwitchCase construct in C or Java, except that patterns are no longer restricted to constants (chars or integers). Given an object (the subject) and a list of patterns, our goal is to find the first pattern that matches the subjects (i.e. that has a compatible shape). More formally, a pattern is a term built over variables and constructors. The latter ones describe the shape of the pattern, whereas the variables are holes that can be instantiated to capture a value. When we consider the term f(a(),g(b())), it has to be viewed as a tree based data-structure with f as a root and a() the first child. Similarly, b() is the unique child of g, which is the second child of the root f . We say that the pattern f(x,y) matches this term (called subject), because we can give values to x and y such that the pattern and the subject become equal: we just have to assign a() to x and g(b()) to y. Finding this assignment is called matching and instantiating. This is exactly what Tom is supposed to do. A pattern may of course contain subterms. Therefore, f(x,g(b())) or f(a(),g(y)) are valid patterns which match against the subject.
Assuming that s is a Java variable, referencing a term (the tree based object f(a(),g(b())) for example), the following Tom construct is valid:
%match(s) {
f(a(),g(y)) -> { /* action 1: code that uses y */ }
f(x,g(b())) -> { /* action 2: code that uses x */ }
f(x,y) -> { /* action 3: code that uses x and y */ }
}
The %match construct is defined as follows:
| MatchConstruct | ::= | ‘%match’ ‘(’ MatchArguments ‘)’ ‘{’ ( PatternAction )* ‘}’ |
| ∣ | ‘%match’ ‘{’ ( ConstraintAction )* ‘}’ | |
| MatchArguments | ::= | [Type] Term ( ‘,’ [Type] Term )* |
| PatternAction | ::= | [LabelName‘:’] PatternList ‘->’ ‘{’ BlockList ‘}’ |
| PatternList | ::= | Pattern( ‘,’ Pattern )* [ (‘&&’ ∣‘||’) Constraint ] |
| ConstraintAction | ::= | Constraint ‘->’ ‘{’ BlockList ‘}’ |
| Constraint | ::= | Pattern ‘<<’ [Type] Term |
| ∣ | Constraint ‘&&’ Constraint | |
| ∣ | Constraint ‘||’ Constraint | |
| ∣ | ‘(’ Constraint ‘)’ | |
| ∣ | Term Operator Term | |
| Operator | ::= | ‘>’ ∣‘>=’ ∣‘<’ ∣‘<=’ ∣‘==’ ∣‘!=’ |
A MatchConstruct is composed of two parts:
Since version 2.6 of the language, an additional syntax, based on constraints, is proposed. In this case, the MatchConstruct can be simply seen as a list of pairs (constraint,action) corresponding to ConstraintAction from the above syntax. For instance, the example we presented before can now be written:
%match {
f(a(),g(y)) << s -> { /* action 1 : code that uses y */ }
f(x,g(b())) << s -> { /* action 2 : code that uses x */ }
f(x,y) << s -> { /* action 3 : code that uses x and y */ }
}
The two versions are semantically equivalent. The expression p << s denotes a match constraint between the pattern p and the subject s. The advantage of this new syntax is the modularity that it offers. For instance, multiple constraints can be combined with the boolean connectors ‘&&’ and ‘||’, leading to a greater expressivity, sometimes closed to the one offered by regular expressions.
The two syntaxes are compatible. For instance the following construct is valid:
%match(s) {
f(a(),g(y)) && ( y << a() || y << b() ) -> { /* action 1 : code that uses y */ }
f(x,g(b())) -> { /* action 2 : code that uses x */ }
}
%match(s) {
f(a(),g(y)) && ( g(z) << y || f(z,_) << y ) -> { /* action 1 : code that uses y and z */ }
f(x,g(b())) && f(y,a()) << someHostFunction(x) -> { /* action 2 : code that uses x and y */ }
}
where someHostFunction can be an arbitrary function from the host language.
if (x == g(a())) {
...
}
For expository reasons, we consider that a %match construct is evaluated in the following way:
The semantics of a match construct may remind the switch/case construct. However, there is a big difference. For instance, in Tom we can have patterns (list-patterns) that can match in several ways a subject. Informally, when considering the subject conc(a(),b(),c()), and the pattern conc(_*,x,_*), there are three possible match for this problem: either x=a(), either x=b(), either x=c(). Note that _* is a special hole which can capture any sublist of conc(…). The list-matching is also known as associative matching. Besides this, some other matching theories are supported in Tom.
When taking this new possibility into account, the evaluation of a %match construct gets a little bit more complex:
As mentioned in the BNF-syntax, a label may be attached to a pattern. In that case, in C and Java, it becomes possible to exit from the current PatternAction (using a goto or a break), without exiting from the whole %match construct. The control is transferred to the next pattern which matches the subjects (respectively to the next constraint). This feature is useful to exit from a complex associative-matching for which, for any reason, we are no longer interested in getting other solutions.
When using the new syntax based on constraints, there are several restrictions that are imposed by the compiler (an error is generated if they are not respected):
As we can imagine, the behavior of a %match construct strongly depends on the patterns which are involved. The formalism which defines the syntax of a pattern is also an essential component of Tom. But because there exist several ways to define patterns with equivalent behavior, its formal definition is not so simple. Although, the different shortcuts help the programmer to simplify the definitions of patterns.
Informally, a pattern is a term built with constructors and variables (please note that x denotes a variable, whereas a() is a constructor). A variable can also be anonymous, and it is denoted by _. Let’s look at some examples of patterns: x, a(), f(a()), g(a(),x), or h(a(),_,x). When a pattern matches a subject, it may be useful to keep a reference to a matched subterm. The annotation mechanism (z@g(y) for example) can be used for this purpose. Thus, considering the matching between the pattern f(x,z@g(y)) and the subject f(a(),g(h(b()))), y is instantiated by h(b()), and z is instantiated by g(h(b())). This can be useful in C, to free the memory for example.
When identical actions have to be performed for a set of patterns which share a common structure, the disjunction of symbols may be used: pattern (f∣g)(a()) is equivalent to the set {f(a()), g(a())}. The disjunction of symbols may also be used in subterms, like in h( (f∣g)(x) ).
More formally, a Tom pattern and a Tom term has the following syntax:
| Term | ::= | VariableName[‘*’] |
| ∣ | Name ‘(’[Term ( ‘,’ Term )*]‘)’ | |
| Pattern | ::= | [ AnnotedName ‘@’ ] PlainPattern |
| PlainPattern | ::= | [‘!’]VariableName [ ‘*’ ] |
| ∣ | [‘!’] HeadSymbolList (ExplicitTermList ∣ ImplicitPairList) | |
| ∣ | ExplicitTermList | |
| ∣ | ‘_’ | |
| ∣ | ‘_*’ | |
| ∣ | XMLTerm | |
| HeadSymbolList | ::= | HeadSymbol [ ‘?’ ] |
| ∣ | ‘(’ HeadSymbol ( ‘∣’ HeadSymbol )+ ‘)’ | |
| ExplicitTermList | ::= | ‘(’ [ Pattern ( ‘,’ Pattern )*] ‘)’ |
| ImplicitPairList | ::= | ‘[’ [ PairPattern ( ‘,’ PairPattern )*] ‘]’ |
| PairPattern | ::= | SlotName ‘=’ Pattern |
Concerning the Term syntax, both Tom and host-language variables can be used and Name can be either a function symbol declared in Tom or the name of a method from the host language.
A pattern is a term which could contain variables.
When matching a pattern against a subject (a ground term), these
variables are instantiated by the matching procedure (generated by
Tom).
In Tom, the variables do not have to be declared: their type is
inferred automatically, depending on the context in which they appear.
As described previously, Tom offers several mechanisms to simplify the definition of a pattern:
In practice, it is usually better to use the disjunction notation with the implicit notation Tom offers: ((f∣g)[arg1=a()]). In that case, the signatures of symbols do not have to be identical: only involved slots have to be common (same names and types). Thus, the pattern (f∣g)[arg1=a()] is correct, even if g has more slots than f: it only has to have the slot arg1, with the same sort.
The use of ‘?’ after a list operator enables real associative with neutral elements (AU) matchings. By using conc? for example, we simply specify that the subject may not start with a conc symbol. For instance, the following code would produce the output matched, because x and respectively y can be instantiated with the neutral element of conc (please see the documentation on Gom for further details about specifying symbols’ type and their neutral elements).
L l = `a();
%match(l) {
conc?(x*,y*) -> { System.out.println("matched"); }
}
Note that without the use of ‘?’, the subject must start with a conc in order to have a match.
The notion of anti-pattern offers more expressive power by allowing complement constructs: a pattern can describe what should not be in the matched subject.
The notion of complement is introduced by the symbol ‘!’, as illustrated by the following grammar fragment:
| PlainPattern | ::= | [‘!’] VariableName |
| ∣ | [‘!’] HeadSymbolList ( ExplicitTermList ∣ ImplicitPairList ) | |
| ∣ | ... |
The semantics of anti-patterns can be best understood when regarding them as complements. For example, a pattern like car[color=blue()] will match all the blue cars. If we add an ‘!’ symbol, the anti-pattern !car[color=blue()] will match everything that is not a blue car, i.e all objects that are not cars or the cars that have a color different from blue. The grammar allows also car[color=!blue()] - matches all cars that are not blue, or !car[color=!blue()] - either everything that is not a car, or a blue car.
Using the non-linearity combined with anti-patterns allows to express interesting searches also. For example, car[interiorColor=x,exteriorColor=x] will match the cars that have the same interior and exterior color. By using the anti-pattern car[interiorColor=x,exteriorColor=!x], the result is as one would expect: it will match all the cars with different interior - exterior colors.
It is also possible to use the anti-patterns in list constructions. Please refer to the tutorial for more examples.
Backquote construct (‘) can be used to build an algebraic term or to retrieve the value of a Tom variable (a variable instantiated by pattern-matching).
| BackQuoteTerm | ::= | [‘‘’] CompositeTerm |
The syntax of CompositeTerm is not fixed since it depends on the underlying language.
However, CompositeTerm should be of the following form:
In general, it is sufficient to add a backquote before the term you want to build to have the desired behavior. The execution of ‘f(g(a())) will build the term f(g(a)), assuming that f, g, and a are Tom operators. Suppose now that g is no longer a constructor but a function of the host-language. The construction ‘f(g(a())) is still valid, but the semantics is the following: the constant a is built, then the function g is called, and the returned result is put under the constructor f. Therefore, the result of g must be a correct term, which belongs to the right type (i.e. the domain of f).
To simplify the interaction with the host-language, it is also possible to use “unknown symbols” like f(x.g()) or f(1+x). The scope of the backquote construct is determined by the scope of the most external enclosing braces, except in two case: ‘x and ‘x* which allow you to use variables instantiated by the pattern part. In that case the scope is limited to the length of the variable name, eventually extended by the ‘’*’’. Sometimes, when writing complex expression like if(‘x==‘y || ‘x==‘z), it can be useful to introduce extra braces (if( ‘(x==y || x==z) )) in order to extend the scope of the backquote.
Tom provides the construct ‘%[’ … ‘]%’ that allows to build formatted strings without the need to encode special characters such as tabulations and carriage returns as it is usually done in Java. For example, to build a string containing the HelloWorld program, one can simply write:
String hello = %[
public class Hello {
public static void main(String[] args) {
System.out.println("Hello\n\tWorld !");
}
}
]%
Additionally, it is possible to insert in this string the content of a String variable, or the result of a function call (if it is a String) using the ‘@’ as escape character: the code contained between ‘@’ in this construct will be evaluated and the result inserted in the surrounding formatted string. Then, to add to the HelloWorld example a version string, we can use:
String version = "v12";
String hello2=%[
public class Hello {
public static void main(String[] args) {
System.out.println("Hello\n\tWorld @version@");
}
}
]%;
Even if the contents of the meta-quote construct is a formatted string, it is required that this string contains correctly balanced braces.
To define the mapping between the algebraic constructors and their concrete implementation, Tom provides a signature-mapping mechanism composed of several constructs. In addition to predefined mapping for usual builtin sorts (int, long, double, boolean, string, and char), all other algebraic sorts have to be declared using the %typeterm construct.
To use predefined sorts (in a %match construct or in the definition of a new operator), it is sufficient to use the %include construct (%include { int.tom } for example).
When defining a new type with the %typeterm construct, some information has to be provided:
Given a Java class Person we can define an algebraic mapping for this class:
%typeterm TomPerson {
implement { Person }
is_sort(t) { t instanceof Person }
equals(t1,t2) { t1.equals(t2) }
}
Here, we assume that the method equals implements a comparison function over instances of Person. Note that we used TomPerson to make a clear distinction between algebraic sorts (defined in Tom) and implementation sorts (defined in Java, via the use of classes). In practice, we usually use the same name to denote both the algebraic sort and the implementation sort.
The grammar is the following:
| IncludeConstruct | ::= | ‘%include’ ‘{’ FileName ‘}’ |
| GomConstruct | ::= | ‘%gom’ [‘(’ optionString ‘)’] ‘{’ GomGrammar ‘}’ |
| GoalLanguageBlock | ::= | ‘{’ BlockList ‘}’ |
| TypeTerm | ::= | ‘%typeterm’ Type ‘{’ |
| KeywordImplement [KeywordIsSort] [KeywordEquals] | ||
| ‘}’ | ||
| KeywordImplement | ::= | ‘implement’ GoalLanguageBlock |
| KeywordIsSort | ::= | ‘is_sort’ GoalLanguageSortCheck |
| KeywordEquals | ::= | ‘equals’ ‘(’ Name ‘,’ Name ‘)’ GoalLanguageBlock |
Once algebraic sorts are declared (using %typeterm), Tom provides a mechanism to define signatures for constructors of these sorts using %op, %oplist or %oparray constructs. When defining a new symbol with the %op construct, the user should specify the name of the operator, its codomain, and its domain. The later one is defined by a list of pairs (slot-name, sort).
Let us consider again the class Person, and let us suppose that an instance of Person has two fields (name and age), we can define the following operator:
%op TomPerson person(name:String, age:int)
In this example, the algebraic operator person has two slots (name and age) respectively of sorts String and int, where String and int are pre-defined sorts.
In addition to the signature of an operator, several auxiliary functions have to be defined:
Coming back to our example, checking if an object t is rooted by the symbol person can be done by checking that t is an instance of the class Person. Building a person can be done via the Java function new Person(...). Accessing to the slots name and age could be implemented by an access to the variables of the class Person. In practice, the following operator definition should work fine:
%op TomPerson person(name:String, age:int) {
is_fsym(t) { t instanceof Person }
make(t1,t2) { new Person(t1,t2) }
get_slot(name,t) { t.name } // assuming that 'name' is public
get_slot(age,t) { t.age } // assuming that 'age' is public
}
When defining a new symbol with the %oplist construct,
the user has to specify how the symbol is implemented.
In addition, the user has to specify how a list can be built and accessed:
Similarly, when defining a new symbol with the %oparray construct, the user has to specify how the symbol is implemented, how an array can be built, and accessed:
Warning: This function should return a list l’ such that the element e is at the end of l.
The %oplist or %oparray is complex but not difficult to use. Let us consider the ArrayList Java class, and let us define a Tom mapping over this data-structure. The first thing to do consists in defining the sort for the elements and the sort for the list-structure:
%typeterm Object {
implement { Object }
equals(l1,l2) { l1.equals(l2) }
}
%typeterm TomList {
implement { ArrayList }
equals(l1,l2) { l1.equals(l2) }
}
Once defined the sorts, it becomes possible to define the list-operator TomList conc( Object* ). This operator has a variadic arity: it takes several Object and returns a TomList.
%oparray TomList conc( Object* ) {
is_fsym(t) { t instanceof ArrayList }
make_empty(n) { new ArrayList(n) }
make_append(e,l) { myAdd(e,(ArrayList)l) }
get_element(l,n) { (Object)l.get(n) }
get_size(l) { l.size() }
}
private static ArrayList myAdd(Object e,ArrayList l) {
l.add(e);
return l;
}
An auxiliary function myAdd is used since the make_append construct should return a new list. The get_element should return an element whose sort belongs to the domain (Object) in this example. Although not needed in this example, in general, a cast ((Object)l.get(n)) is needed.
The grammar for the mapping constructs is the following:
| Operator | ::= | ‘%op’ Type Name |
| ‘(’ [ SlotName ‘:’ Type ( ‘,’ SlotName ‘:’ Type )* ] ‘)’ | ||
| ‘{’ KeywordIsFsym ( KeywordMake ∣ KeywordGetSlot )* ‘}’ | ||
| OperatorList | ::= | ‘%oplist’ Type Name ‘(’ Type ‘*’ ‘)’ |
| ‘{’ KeywordIsFsym ( KeywordMakeEmptyList | ||
| ∣ KeywordMakeInsert ∣ KeywordGetHead | ||
| ∣ KeywordGetTail ∣ KeywordIsEmpty )* ‘}’ | ||
| OperatorArray | ::= | ‘%oparray’ Type Name ‘(’ Type ‘*’ ‘)’ |
| ‘{’ KeywordIsFsym ( KeywordMakeEmptyArray ∣ | ||
| KeywordMakeAppend ∣ KeywordElement | ||
| ∣ KeywordGetSize )* ‘}’ | ||
| KeywordIsFsym | ::= | ‘is_fsym’ ‘(’ Name ‘)’ GoalLanguageBlock |
| KeywordGetSlot | ::= | ‘get_slot’ ‘(’ Name ‘,’ Name ‘)’ GoalLanguageBlock |
| KeywordMake | ::= | ‘make’ [ ‘(’ Name ( ‘,’ Name )* ‘)’ ] GoalLanguageBlock |
| KeywordGetHead | ::= | ‘get_head’ ‘(’ Name ‘)’ GoalLanguageBlock |
| KeywordGetTail | ::= | ‘get_tail’ ‘(’ Name ‘)’ GoalLanguageBlock |
| KeywordIsEmpty | ::= | ‘is_empty’ ‘(’ Name ‘)’ GoalLanguageBlock |
| KeywordMakeEmptyList | ::= | ‘make_empty’ [ ‘(’ ‘)’ ] GoalLanguageBlock |
| KeywordMakeInsert | ::= | ‘make_insert’ ‘(’ Name ‘,’ Name ‘)’ GoalLanguageBlock |
| KeywordGetElement | ::= | ‘get_element’ ‘(’ Name ‘,’ Name ‘)’ GoalLanguageBlock |
| KeywordGetSize | ::= | ‘get_size’ ‘(’ Name ‘)’ GoalLanguageBlock |
| KeywordMakeEmptyArray | ::= | ‘make_empty’ ‘(’ Name ‘)’ GoalLanguageBlock |
| KeywordMakeAppend | ::= | ‘make_append’ ‘(’ Name ‘,’ Name ‘)’ GoalLanguageBlock |
See Section 13.1.
The grammar for the Gom construct is as follows:
| GomConstruct | ::= | ‘%gom’ [‘(’ optionString ‘)’] ‘{’ GomGrammar ‘}’ |
It allows to define a Gom signature (for more details about Gom see Chapter 11). The Gom compiler is called on the GomGrammar, and the construct is replaced by the produced Tom mapping. The optionString is composed by a list of command line options to pass to the underlying Gom compiler, as described in section 16.1.
To deal with XML documents, the XML notation can be used (<A><B attribute="name"/></A> for example).
When manipulating XML documents, we distinguish two main kinds of operations: retrieving information and transforming a document. Tom provides three different XML notations that ought to simplify the definition of patterns: the “standard ” and the “implicit” XML notations are used to define compact (but incomplete) patterns. This notation is well suited to retrieve information. The “explicit” XML notation is used to precisely describe an XML pattern and all the variables that have to be instantiated. This notation is particularly well suited to perform XML transformation since it allows the programmer to precisely describe how variables have to be instantiated.
To make the XML notation understandable, we have to explain how XML documents are handled by Tom. To each XML document corresponds a DOM (Document Object Model) representation. In Tom, we have defined a mapping from DOM sorts to abstract algebraic sorts: TNode and TNodeList, which correspond respectively to Node and NodeList, defined by the Java DOM implementation.
Thus, a Node object becomes a ternary operator Element whose first subterm is the name of the XML node, the second subterm is a list of attributes and the third subterm is a list of subterms (which correspond to XML sub-elements). The second and the third elements are terms of sort TNodeList (because they are implemented by NodeList objects in DOM).
Thus, when considering the <A></A> XML document, the corresponding algebraic term is Element("A",[],[]), where [] denotes the empty list. Similarly, <A><B attribute="name"/></A> is encoded into Element("A",[],[Element("B",[Attribute("attribute","name")],[])]).
When defining an XML pattern, the user has to introduce extra list-variables to precisely describe the XML pattern and capture the different contexts. Suppose that we are interested in finding a node <B></B> which is a subterm of a node <A></A> (but not necessary the first subterm). The algebraic pattern should be Element("A",[_*],[_*,Element("B",[_*],[_*]),_*]). Using the XML notation, this pattern should be expressed as follows: <A(_*)>(_*,<B(_*)>(_*)</B>,_*)</A>. This notation (called explicit) is precise but error prone. This is why we have introduced the explicit notation, where all context variable can be removed (and () are replaced by []): <A[]><B[]>[]</B></A>. The last notation (called standard XML notation) allows the user to remove the [] and replace the list-separator (,) by spaces. The previous pattern can be written: <A><B></B></A>.
These three different notations allow the user to choose the level of control he wants to have on the XML pattern matching algorithm.
The formal description of the syntax is the following:
| XMLTerm | ::= | ‘<’ XMLNameList XMLAttrList ‘/>’ |
| ∣ | ‘<’ XMLNameList XMLAttrList ‘>’ XMLChilds ‘</’ XMLNameList ‘>’ | |
| ∣ | ‘#TEXT’ ‘(’ Identifier ∣ String ‘)’ | |
| ∣ | ‘#COMMENT’ ‘(’ Identifier ∣ String ‘)’ | |
| ∣ | ‘#PROCESSING-INSTRUCTION’ | |
| ‘(’ (Identifier ∣ String) ‘,’ (Identifier ∣ String) ‘)’ | ||
| XMLNameList | ::= | XMLName |
| ∣ | ‘(’ XMLName ( ‘∣’ XMLName )* ‘)’ | |
| XMLAttrList | ::= | ‘[’ [ XMLAttribute (‘,’ XMLAttribute)* ] ‘]’ |
| ∣ | ‘(’ [ XMLAttribute (‘,’ XMLAttribute)* ] ‘)’ | |
| ∣ | ( XMLAttribute )* | |
| XMLAttribute | ::= | ‘_*’ |
| ∣ | VariableName ‘*’ | |
| ∣ | AttributeName ‘=’ [AnnotedName ‘@’] ( Identifier ∣ String ) | |
| ∣ | [AnnotedName ‘@’] ‘_’ ‘=’ [AnnotedName ‘@’] ( Identifier ∣ String ) | |
| XMLChilds | ::= | ( Term )* |
| ∣ | ‘[’ Term ( ‘,’ Term )* ‘]’ |
Gom is a generator of tree implementations in Java, allowing the definition of a preferred canonical form, using hooks. The tree implementations Gom generates are characterized by strong typing, immutability (there is no way to manipulate them with side-effects), maximal subterm sharing and the ability to be used with strategies.
The basic functionality of Gom is to provide a tree implementation in Java corresponding to an algebraic specification.
Gom provides a syntax to concisely define abstract syntax tree, which is inspired from the algebraic type definition of ML languages.
Each Gom file consists in the definition of one or more modules. In each module we define sorts, and operators for the sorts. Additionally, it allows to define hooks modifying the default behavior of an operator.
| GomGrammar | ::= | Module |
| Module | ::= | ‘module’ ModuleName [Imports] Grammar |
| Imports | ::= | ‘imports’ (ModuleName)* |
| Grammar | ::= | ‘abstract syntax’ (TypeDefinition ∣ HookDefinition)* |
| TypeDefinition | ::= | SortName ‘=’ [‘|’] OperatorDefinition (‘|’ OperatorDefinition)* |
| OperatorDefinition | ::= | OperatorName ‘(’[SlotDefinition(‘,’SlotDefinition)*]‘)’ |
| ∣ | OperatorName ‘(’ SortName‘*’ ‘)’ | |
| SlotDefinition | ::= | SlotName ‘:’ SortName |
| ModuleName | ::= | Identifier |
| SortName | ::= | Identifier |
| OperatorName | ::= | Identifier |
| SlotName | ::= | Identifier |
| HookDefinition | ::= | HookType ‘:’ HookOperation |
| HookType | ::= | OperatorName |
| ∣ | ‘module’ ModuleName | |
| ∣ | ‘sort’ SortName | |
| HookOperation | ::= | ‘make’ ‘(’ [Identifier (‘,’ Identifier)*] ‘)’ ‘{’ TomCode ‘}’ |
| ∣ | ‘make_insert’ ‘(’ Identifier ‘,’ Identifier)* ‘)’ ‘{’ TomCode ‘}’ | |
| ∣ | ‘make_empty’ ‘(’‘)’ ‘{’ TomCode ‘}’ | |
| ∣ | ‘Free () {}’ | |
| ∣ | ‘FL () {}’ | |
| ∣ | (‘AU’ ∣‘ACU’) ‘()’ ‘{’ [‘‘’ term] ‘}’ | |
| ∣ | ‘interface()’ ‘{’ Identifier (‘,’ Identifier )* ‘}’ | |
| ∣ | ‘import()’ ‘{’ JavaImports ‘}’ | |
| ∣ | ‘block()’ ‘{’ TomCode ‘}’ | |
| ∣ | ‘rules()’ ‘{’ RulesCode ‘}’ | |
| ∣ | ‘graphrules(’ Identifier ‘,’ (‘Identity’ ∣‘Fail’)‘)’‘{’ GraphRulesCode ‘}’ | |
| RulesCode | ::= | (Rule)* |
| Rule | ::= | RulePattern ‘->’ TomTerm [‘if’ Condition] |
| RulePattern | ::= | [ AnnotedName ‘@’ ] PlainRulePattern |
| PlainRulePattern | ::= | [‘!’]VariableName [ ‘*’ ] |
| ∣ | [‘!’]HeadSymbolList ‘(’ [RulePattern ( ‘,’ RulePattern )*] ‘)’ | |
| ∣ | ‘_’ | |
| ∣ | ‘_*’ | |
| GraphRulesCode | ::= | (GraphRule)* |
| GraphRule | ::= | TermGraph ‘->’ TermGraph [‘if’ Condition] |
| TermGraph | ::= | [ Label ‘:’ ] TermGraph |
| ∣ | ‘&’ Label | |
| ∣ | VariableName [ ‘*’ ] | |
| ∣ | HeadSymbolList ‘(’ [TermGraph ( ‘,’ TermGraph )*] ‘)’ | |
| Label | ::= | Identifier |
| Condition | ::= | TomTerm Operator TomTerm |
| ∣ | RulePattern ‘<<’ TomTerm | |
| ∣ | Condition ‘&&’ Condition | |
| ∣ | Condition ‘||’ Condition | |
| ∣ | ‘(’ Condition ‘)’ | |
| Operator | ::= | ‘>’ ∣‘>=’ ∣‘<’ ∣‘<=’ ∣‘==’ ∣‘!=’ |
Gom supports several builtin sorts, that may be used as sort for new operators slots. To each of these builtin sorts corresponds a Java type. Native data types from Java can be used as builtin fields, as well as ATerm and ATermList structures. To use one of these builtin types in a Gom specification, it is required to add an import for the corresponding builtin.
| Name | Java type |
| int | int |
| String | String |
| char | char |
| double | double |
| long | long |
| float | float |
| ATerm | aterm.ATerm |
| ATermList | aterm.ATermList |
It is not possible to define a new operator whose domain is one of the builtin sorts, since those sorts are defined in another module.
External Gom modules may be imported in a Gom specification, by adding the name of the module to import in the ‘imports’ section. Once a module imported, it is possible to use any of the sorts this module declares or imports itself as type for a new operator slot. Adding new operators to an imported sort is however not allowed.
The syntax of Gom is quite simple and can be used to define many-sorted abstract-datatypes. The module section defines the name of the signature. The imports section defines the name of the imported signatures. The abstract syntax part defines the operators with their signature. For each argument, a sort and a name (called slot-name) has to be given.
module Expressions
imports String int
abstract syntax
Bool = True()
| False()
| Eq(lhs:Expr, rhs:Expr)
Expr = Id(stringValue:String)
| Nat(intValue:int)
| Add(lhs:Expr, rhs:Expr)
| Mul(lhs:Expr, rhs:Expr)
The definition of a signature in Gom has several restrictions:
A first solution to combine Tom with Gom is to use Gom as a standalone tool, using the command line tool or the ant task.
In that case, the module name of the Gom specification and the package option determine where the files are generated. To make things correct, it is sufficient to import the generated Java classes, as well as the generated Tom file. In the case of a Gom module called Module, all files are generated in a directory named module and the Tom program should do the following:
import module.*;
import module.types.*;
class MyClass {
...
%include { module/Module.tom }
...
}
A second possibility to combine Tom with Gom is to use the %gom construct offered by Tom. In that case, the Gom module can be directly included into the Tom file, using the %gom instruction:
package myPackage;
import myPackage.myclass.expressions.*;
import myPackage.myclass.expressions.types.*;
class MyClass {
%gom{
module Expressions
abstract syntax
Bool = True()
| False()
...
Expr = Mul(lhs:Expr, rhs:Expr)
}
...
}
Note that the Java code is generated in a package that corresponds to the current package, followed by the class-name and the module-name. This allows to define the same module in several classes, and avoid name clashes.
Gom provides hooks that allow to define properties of the data-structure, in particular canonical forms for the terms in the signature in an algebraic way.
The ‘rules’ hook ables to define a set of conditional rewrite rules over the current module signature. Those rules are applied systematically using a leftmost innermost strategy. Thus, the only terms that can be produced and manipulated in the Tom program are normal with respect to the defined system.
module Expressions
imports String int
abstract syntax
Bool = True()
| False()
| Eq(lhs:Expr, rhs:Expr)
Expr = Id(stringValue:String)
| Nat(intValue:int)
| Add(lhs:Expr, rhs:Expr)
| Mul(lhs:Expr, rhs:Expr)
module Expressions:rules() {
Eq(x,x) -> True()
Eq(x,y) -> False() if x!=y
}
Since the rules do alter the behavior of the construction functions in the term structure, it is required in a module that the rules in a ‘rules’ hook have as left hand side a pattern rooted by an operator of the current module. The rules are tried in the order of their definitions, and the first matching rule is applied.
Hooks may be used to specify how operators should be created. ‘make’, ‘make_empty’ and ‘make_insert’ hooks are altering the creation operations for respectively algebraic, neutral element (empty variadic) and variadic operators. ‘make_insert’ is simply a derivative case of ‘make’, with two arguments, for variadic operators.
The hook operation type is followed by a list of arguments name between ‘()’. The creation operation takes those arguments in order to build a new instance of the operator. Thus, the arguments number has to match the slot number of the operator definition, and types are inferred from this definition.
Then the body of the hook definition is composed of Java and Tom code. The Tom code is compiled using the mapping definition for the current module, and thus allows to build and match terms from the current module. This code can also use the realMake function, which consists in the "inner" default allocation function. This function takes the same number of arguments as the hook. In any case, if the hooks code does not perform a return itself, this realMake function is called at the end of the hook execution, with the corresponding hooks arguments
Using the expression example introduced in 11.1.2, we can add hooks to implement the computation of Add and Mul when both arguments are known integers (i.e. when they are Nat(x))
module Expressions
imports String int
abstract syntax
Bool = True()
| False()
| Eq(lhs:Expr, rhs:Expr)
Expr = Id(stringValue:String)
| Nat(intValue:int)
| Add(lhs:Expr, rhs:Expr)
| Mul(lhs:Expr, rhs:Expr)
Add:make(l,r) {
%match(Expr l, Expr r) {
Nat(lvalue), Nat(rvalue) -> {
return `Nat(lvalue + rvalue);
}
}
}
Mul:make(l,r) {
%match(Expr l, Expr r) {
Nat(lvalue), Nat(rvalue) -> {
return `Nat(lvalue * rvalue);
}
}
}
Using this definition, it is impossible to have an expression containing unevaluated expressions where a value can be calculated. Thus, a procedure doing constant propagations for Id whose value is known could simply replace the Id by the corresponding Nat, and rely on this mechanism to evaluate the expression. Note that the arguments of the make hook are themselves elements built on this signature, and thus the hooks have been applied for them. In the case of hooks encoding a rewrite system, this corresponds to using an innermost strategy.
In order to ease the use of variadic operators with the same domain and co-domain, Gom does provide hooks that enforce a particular canonical form for lists.
<op>:FL() {}, ensures that structures
containing the operator <op> are left to right combs, with an empty
<op>() at the right.
This constitutes a particular form of associative with neutral element
canonical form, with a restriction on the application of the neutral rules.
This corresponds to the generation of the following normalisation rules:
make(Empty,tail) -> tail make(Cons(h,t),tail) -> make(h,make(t,tail)) make(head,tail) -> make(head,make(tail,Empty)) if tail!=Empty and tail!=Cons
<op>:Free() {}, ensures the variadic
symbol remains free, i.e. deactivates the default FL hook.
<op>:AU() {}, ensures that structures
containing the <op> operator are left to right comb, and that neutral
elements are removed. It is possible to specify an alternate neutral element
to the associative with neutral theory, using <op>:AU() {`<elem>()},
where <elem> is a term in the signature.
This will generate the following normalisation rules:
make(Empty,tail) -> tail make(head,Empty) -> head make(Cons(h,t),tail) -> make(h,make(t,tail))
make(Empty,tail) -> tail make(head,Empty) -> head make(Cons(h,t),tail) -> make(h,make(t,tail)) make(head,Cons(h,t)) -> make(head,Cons(h,t)) if head < h make(head,Cons(h,t)) -> make(h,make(head,t)) if head >= h
If you do not define any hook of the form AU, ACU, FL, Free, or rules, the FL hook will be automatically declared for variadic operators those domain and co-domain are equals. In practice, this makes list matching and associative matching with neutral element easy to use.
If you use a hook rules, there may be an interaction that can lead to non-termination. Therefore, no hook will be automatically added, and you are forced to declare a hook of the form AU, ACU, FL or Free.
For each Module, the Gom compiler generates an API specific of this module, possibly using the API of other modules (declared in the Imports section). This API is located in a Java package named using the ModuleName lowercased, and contains the tree implementation itself, with some additional utilities:
public aterm.ATerm toATerm(); public String symbolName(); public int compareTo(Object o); public int compareToLPO(Object o); public void toStringBuilder(java.lang.StringBuilder buffer);
public boolean is<op>(); public <SlotType> get<slotName>(); public <SortName> set<slotName>(<SlotType>); public static <SortName> fromTerm(aterm.ATerm trm); public static <SortName> fromString(String s); public static <SortName> fromStream(java.io.InputStream stream) throws java.io.IOException; public int length(); public <SortName> reverse();
public static <op> make(arg1,...,argn);
We show elements of the generated API for a very simple example, featuring variadic operator. It defines natural numbers as Zero() and Suc(n), and lists of natural numbers.
module Mod
abstract syntax
Nat = Zero()
| Suc(pred:Nat)
| Plus(lhs:Nat,rhs:Nat)
| List(Nat*)
Using the command gom Mod.gom, the list of generated files is:
mod/Mod.tom (the Tom mapping) mod/ModAbstractType.java mod/types/Nat.java (abstract class for the "Nat" sort) mod/types/nat/List.java \ mod/types/nat/ConsList.java \ mod/types/nat/EmptyList.java / Implementation for the operator "List" mod/types/nat/Plus.java (Implementation for "Plus") mod/types/nat/Suc.java (Implementation for "Suc") mod/types/nat/Zero.java (Implementation for "Zero")
The ModAbstractType class declares generic methods shared by all operators in the Mod module:
public aterm.ATerm toATerm() public String symbolName() public String toString()
The mod/types/Nat.java class provides an abstract class for all operators in the Nat sort, implementing the ModAbstractType and contains the following methods. First, the methods for checking the root operator, returning false by default:
public boolean isConsList() public boolean isEmptyList() public boolean isPlus() public boolean isSuc() public boolean isZero()
Then getter methods, throwing an UnsupportedOperationException by default, as the slot may not be present in all operators. This is convenient since at the user level, we usually manipulate objects of sort Nat, without casting them to more specific types.
public mod.types.Nat getpred() public mod.types.Nat getlhs() public mod.types.Nat getHeadList() public mod.types.Nat getrhs() public mod.types.Nat getTailList()
The fromTerm static method allows Gom data structure to be
interoperable with ATerm
public static mod.types.Nat fromTerm(aterm.ATerm trm)
The operator implementations redefine all or some getters for the operator to return its subterms. It also provides a static make method to build a new tree rooted by this operator, and implements the tom.library.sl.Visitable interface. For instance, in the case of the Plus operator, the interface is:
public static Plus make(mod.types.Nat lhs, mod.types.Nat rhs) public int getChildCount() public tom.library.sl.Visitable getChildAt(int index) public tom.library.sl.Visitable setChildAt(int index, tom.library.sl.Visitable v)
completed with the methods from the Nat class and the ModAbstractType.
The operators implementing the variadic operator both extend the List class, which provides list related methods, such as length, toArray and reverse. The toArray method produces an array of object of the codomain type corresponding to the list elements, while the reverse method returns the list with all elements in reverse order. The List class for our example then contains:
public int length() public mod.types.Nat[] toArray() public mod.types.Nat reverse()
For the ConsList class, we obtain:
/* the constructor */
public static ConsList make(mod.types.Nat _HeadList, mod.types.Nat _TailList) { ... }
public String symbolName() { ... }
/* From the "Nat" class */
public boolean isConsList() { ... }
public mod.types.Nat getHeadList() { ... }
public mod.types.Nat getTailList() { ... }
/* From the "ModAbstractType" class */
public aterm.ATerm toATerm() { ... }
public static mod.types.Nat fromTerm(aterm.ATerm trm) { ... }
/* The tom.library.sl.Visitable interface */
public int getChildCount() { ... }
public tom.library.sl.Visitable getChildAt(int index) { ... }
public tom.library.sl.Visitable setChildAt(int index, tom.library.sl.Visitable v) { ... }
/* The MuVisitable interface */
public tom.library.sl.Visitable setChilds(tom.library.sl.Visitable[] childs) { ... }
There exist four other hooks ‘import’, ‘interface’, ‘block’ and ‘mapping’ that offer possibilities to enrich the generated API. Contrary to ‘make’ and ‘make_insert’, these hooks have no parameters. Moreover, they can be associated not only to an operator but also to a module or a sort.
| HookDefinition | ::= | HookType ‘:’ HookOperation |
| HookType | ::= | OperatorName |
| ∣ | ‘module’ ModuleName | |
| ∣ | ‘sort’ SortName | |
| HookOperation | ::= | ‘interface()’ ‘{’ Identifier (‘,’ Identifier )* ‘}’ |
| ∣ | ‘import()’ ‘{’ JavaImports ‘}’ | |
| ∣ | ‘block()’ ‘{’ TomCode ‘}’ | |
| ∣ | ‘mapping()’ ‘{’ TomMapping ‘}’ |
There are few constraints on the form of the code in these hooks:
The code given in the hook is just added at the correct position in the corresponding Java class:
In the case of ‘mapping’ hooks, the corresponding code is added to the mapping generated for the signature.
module Expressions
imports String int
abstract syntax
Bool = True()
| False()
| Eq(lhs:Expr, rhs:Expr)
Expr = Id(stringValue:String)
| Nat(intValue:int)
| Add(lhs:Expr, rhs:Expr)
| Mul(lhs:Expr, rhs:Expr)
True:import() {
import tom.library.sl.*;
import java.util.HashMap;
}
sort Bool:interface() { Cloneable, Comparable }
module Expressions:block() {
%include{ util/HashMap.tom }
%include{ sl.tom }
%strategy CollectIds(table:HashMap) extends Identity() {
visit Expr {
Id(value) -> {
table.put(`value,getEnvironment().getPosition());
}
}
}
public static HashMap collect(Expr t) {
HashMap table = new HashMap();
`TopDown(CollectIds(table)).apply(t);
return table;
}
}
A term-graph is a term where subterms can be shared and where there may be cycles. Gom offers support to define term-graphs and term-graph rule systems. There exist several ways to define term-graphs but in our case, we propose to represent term-graphs by terms with pointers. These pointers are defined by a relative path inside the term. All the formal definitions can be found in this paper.
When defining a Gom algebraic signature, it is possible to construct term-graphs on these signature using the option –termgraph. In this case, the signature is automatically extended to manage labels. For every sort T, two new constructors are added:
LabT(label:String,term:T) RefT(label:String)
With these two new constructors, users can define term-graphs as labelled terms:
Term cyclicTerm = `LabTerm("l",f(RefTerm("l")));
Term termWithSharing = `g(RefTerm("a"),LabTerm("a",a()));
From this labelled term, users can obtain the term-graph representation with paths using the expand method. This method must be called before applying a term-graph strategy.
Using the hook graphrules, it is possible to define a set of term-graph rules. The left-hand and right-hand sides of these rules are term-graphs. A set of rules can only be associated to a given sort.
sort Term: graphrules(MyGraphStrat,Identity) {
g(l:a(),&l) -> f(b())
f(g(g(a(),&l),l:x)) -> g(ll:b(),&ll) if b()<<x
}
In the rules, sharings and cycles are not represented by the constructor LabTerm and RefTerm but using a light syntax. l:t is equivalent to LabTerm(l,t) and &l corresponds to RefTerm(l).
Contrary to classical term-graph rewriting, it is possible to reuse a label from the left-hand side in the right-hand side in order to obtain side effects. This feature is inspired from Rachid Echahed’s formalism.
sort Term: graphrules(SideEffect,Identity) {
f(l:a()) -> g(&l,l:b())
}
This set of rules is translated into a Tom %strategy that can be used in a Tom program:
Term t = (Term) `g(RefTerm("a"),LabTerm("a",a())).expand();
`TopDown(Term.MyGraphStrat()).visit(t)
The data structures generated by Gom do provide support for the strategy language of Tom. We assume in this section the reader is familiar with the strategies support of Tom as described in chapter 12, and illustrated in chapter 7 of the tutorial.
The data structure generated by the Gom compiler provide support for the sl library implementing strategies for Tom. It is thus possible without any further manipulation to use the strategy language with Gom data structures.
This strategy support is extended by the Gom generator by providing congruence and construction elementary strategies for all operators of the data structure. Those strategies are made available through a Tom mapping _<module>.tom generated during Gom compilation.
The congruence strategies are generated for each operator in the Gom module. For a module containing a sort
Term = | a()
| f(lt:Term,rt:Term)
congruence strategies are generated for both a and f operators, respectively called _a and _f. The semantics of those elementary strategies is as follows:
| (_a)[t] | ⇒ | t if t equals a, failure otherwise |
| (_f(s1,s2))[t] | ⇒ | f(t1’,t2’) if t = f(t1,t2), with (s1)[t1] ⇒t1’ and (s2)[t2] ⇒t2’, |
| failure otherwise |
Thus, congruence strategies allows to discriminate terms based on how they are built, and to develop strategies adopting different behaviors depending on the shape of the term they are applied to.
Congruence strategies are commonly used to implement a specific behavior depending on the context (thus, it behaves like a complement to pattern matching). For instance, to print all first children of an operator f, it is possible to use a generic Print() strategy under a congruence operator.
Strategy specPrint = `TopDown(_f(Print(),Identity()));
Also, congruence strategies are used to implement map like strategies on tree structures:
Strategy map(Strategy arg) {
return `mu(MuVar("x"),
Choice(_Empty(),_Cons(arg,MuVar("x")))
);
}
The congruence strategy generated for variadic operators is similar to the map strategy, and will apply its argument to all subterms of a variadic operator.
Gom generated strategies’ purpose is to allow to build new terms for the signature at the strategy level. Those strategies do not use the terms they are applied to, and simply create a new term. Their semantics is as follows:
| (Make_a)[t] | ⇒ | a |
| (Make_f(s1,s2))[t] | ⇒ | f(t1,t2) if (s1)[null] ⇒t1 and (s2)[null] ⇒t2, |
| failure otherwise |
We can note that as the sub-strategies for Make_f are applied to the null term, it is required that those strategies are themselves construction strategies and do not examine their argument.
These construction strategies, combined with congruence strategies can be used to implement rewrite rules as strategies. For instance, a rule f(a,b) → g(a,b) can be implemented by the strategy:
Strategy rule = `Sequence( _f(_a(),_b()), _Make_g(_Make_a(),_Make_b()) );
To exercise some control over the application of the rules, rewriting based languages provide abstract ways by using reflexivity and the meta-level for Maude, or the notion of rewriting strategies as in Tom. Strategies such as bottom-up, top-down or leftmost-innermost are higher-order features that describe how rewrite rules should be applied (At each step, the strategy chooses which rule is applied and in which position inside the term).
In Tom, we have developed a flexible and expressive strategy language inspired by ELAN, Stratego, and JJTraveler where high-level strategies are defined by combining low-level primitives. For example, the top-down strategy is recursively defined by Sequence(s,All(TopDown(s))). Users can define elementary strategies (corresponding to a set of rewriting rules) and control them using various combinators proposed in the sl library. This rich strategy language allows to easily define various kinds of term traversals.
In this chapter, first, we briefly present the sl library functioning. After that, we describe in detail every elementary strategies and strategy combinators. Then, we explain how the sl library can be used in combination with Gom structures.
The package tom.library.sl is mainly composed by an interface Strategy and a class for each strategy combinator.
Every strategy (elementary strategies or combinators) implements the Strategy interface. To apply a strategy on a term (generally called the subject), this interface offers two methods:
A strategy can visit any Visitable object. Any term constructed using a Tom mapping or a Gom signature is Visitable. The first method visitLight is the most efficient because it does not manage any environment. Most of time, it is sufficient.The second method depends on an environment (see Section 12.1.2). The visit(Visitable) method behaves like visitLight but updates at each step an environment.
When applying on a term, a strategy returns a Visitable corresponding to the result. In case of failures, these two methods throw a VisitFailure exception.
An environment is composed of the current position and the current subterm where the strategy is applied. This object corresponds to the class Environment of the package tom.library.sl and can be associated to a strategy using setEnvironment(Environment) and accessed using getEnvitonment(). A position in a term is a sequence of integers that represents the path from the root of the term to the current subterm where the strategy is applied.
The method getPosition() in the Environment class returns a Position object that represents the current position. Due to the method getSubject(), users can also get the current subterm where the strategy is applied.
To retrieve all this information from a strategy, the visit method is necessary.
An elementary strategy corresponds to a minimal transformation. It could be Identity (does nothing), Fail (always fails), or a set of rewrite rules (performs an elementary rewrite step only at the root position). In our system, strategies are type-preserving and have a default behavior (introduced by the keyword extends)
The first two elementary strategies are the identity and the failure. There are defined by two corresponding classes in sl library: Identity and Fail. These two strategies have no effect on the term. The identity strategy returns the term unchanged. The failure strategy throws a VisitFailure exception.
Users can define elementary strategies by using the %strategy construction. This corresponds to a list of MatchStatement (one associated to each sort) and can be schematically seen as a set of rewriting rules.
Here is the %strategy grammar:
| StrategyConstruct | ::= | ‘%strategy’ StrategyName ‘(’ [StrategyArguments] ‘)’ |
| ‘extends’ [‘‘’] Term ‘{’ StrategyVisitList ‘}’ | ||
| StrategyArguments | ::= | SubjectName ‘:’ AlgebraicType ( ‘,’ SubjectName ‘:’ AlgebraicType )* |
| ∣AlgebraicType SubjectName ( ‘,’ AlgebraicType SubjectName )* | ||
| StrategyVisitList | ::= | ( StrategyVisit )* |
| StrategyVisit | ::= | ‘visit’ AlgebraicType ‘{’ ( VisitAction )* ‘}’ |
| VisitAction | ::= | [LabelName‘:’] PatternList ‘->’ (‘{’ BlockList ‘}’ ∣Term) |
This strategy has a name, followed with mandatory parenthesis. Inside these parenthesis, we have optional parameters.
The strategy has an extendsTerm which defines the behavior of the default strategy that will be applied. In most cases, two default behaviours are used:
Note that this default behaviour is executed if no rule can be applied or if there is no Java return statement executed in the applied rules.
The body of the strategy is a list of visited sorts. Each StrategyVisit contains a list of VisitAction that will be applied to the corresponding sort. A VisitAction is either a PatternAction or simply a Term (equivalent to the VisitAction { return Term;}). In other words, a StrategyVisit is translated into a MatchStatement.
For instance, here is an elementary strategy RewriteSystem that can be instantiated as follows:
%strategy RewriteSystem() extends Identity() {
visit Term {
a() -> { return `b(); }
b() -> { return `c(); }
}
}
Strategy rule = `RewriteSystem();
%include { util/types/HashSet.tom }
%strategy RewriteSystem(hs:HashSet) extends Identity() {
visit Term {
a() -> { hs.add(`a()); }
b() -> { return `c(); }
}
}
The RewriteSystem strategy can be instantiated as follows:
HashSet hashset = new HashSet(); Strategy rule =`RewriteSystem(hashset);
Strategies defined by ‘%strategy’ are local to the file defining them. If you want to export your strategy to another package, you have to create a public function exporting an instance of the strategy built with ‘‘’.
The following operators are the key-component that can be used to define more complex strategies. In this framework, the application of a strategy to a term can fail. In Java, the failure is implemented by an exception (VisitFailure) of the package library.sl.
| (Identity)[t] | ⇒ | t |
| (Fail)[t] | ⇒ | failure |
| (Sequence(s1,s2))[t] | ⇒ | failure if (s1)[t] fails |
| (s2)[t’] if (s1)[t] ⇒t’ | ||
| (Choice(s1,s2))[t] | ⇒ | t’ if (s1)[t] ⇒t’ |
| (s2)[t] if (s1)[t] fails | ||
| (All(s))[f(t1,...,tn)] | ⇒ | f(t1’,...,tn’) if (s)[t1] ⇒t1’, ..., (s)[tn] ⇒tn’ |
| failure if there exists i such that (s)[ti] fails | ||
| (All(s))[cst] | ⇒ | c |
| (One(s))[f(t1,...,tn)] | ⇒ | f(t1,...,ti’,...,tn) if (s)[ti] ⇒ti’ |
| failure (s)[t1] fails, ..., (s)[tn] fails | ||
| (One(s))[cst] | ⇒ | failure |
For example, we can define myFirstStrat = ‘All(RewriteSystem) where Rewritesystem is defined as the elementary strategy:
%strategy RewriteSystem() extends Fail() {
visit Term {
a() -> { return `b(); }
}
}
When applying this strategy to different subjects, we obtain:
| (myFirstStrat)[f(a(),a())] | ⇒ | f(b(),b()) |
| (myFirstStrat)[f(a(),b())] | ⇒ | failure |
| (myFirstStrat)[b()] | ⇒ | b() |
Sometimes, it is interesting to get the environment where the strategy is applied. The interface Strategy each strategy do implement provides a method getEnvironment() to get the current environment of the strategy. In particular, it is interesting when you want to collect the current position where the strategy is applied. In this case, you can call getEnvironment().getPosition().
This information is also available through the getEnvironment() method from the AbstractStrategy class. To use this method or the following strategies which depend on it, you must call the visit method on your strategy instead of visitLight. That is the difference between visitLight and visit. Only the visit method maintain an environment.
try {
Strategy s = `OnceBottomUp(rule);
s.visit(subject));
} catch(VisitFailure e) {
System.out.prinltn("Failure at position" + s.getEnvironment().getPosition());
}
The library gives several basic strategies using the position:
| (Omega(i,s))[f(t1,...,tn)] | ⇒ | f(t1,...,ti’,...,tn) if (s)[ti] ⇒ti’ |
| failure if (s)[ti] fails | ||
| (getEnvironment().getPosition().getReplace(i,t))[f(t1,...,tn)] | ⇒ | f(t1,...,t,...,tn) |
| (getEnvironment().getPosition().getSubterm(i,t))[f(t1,...,tn)] | ⇒ | ti |
In order to define recursive strategies, we introduce the µ abstractor. This allows to give a name to the current strategy, which can be referenced later.
| Try(s) | = | Choice(s,Identity) |
| Repeat(s) | = | µ x.Choice(Sequence(s,x),Identity()) |
| OnceBottomUp(s) | = | µ x.Choice(One(x),s)) |
| BottomUp(s) | = | µ x.Sequence(All(x),s)) |
| TopDown(s) | = | µ x.Sequence(s,All(x))) |
| Innermost(s) | = | µ x.Sequence(All(x),Try(Sequence(s,x)))) |
The Try strategy never fails: it tries to apply the strategy s. If it succeeds, the result is returned. Otherwise,the Identity strategy is applied, and the subject is not modified.
The Repeat strategy applies the strategy s as many times as possible, until a failure occurs. The last unfailing result is returned.
The strategy OnceBottomUp tries to apply the strategy s once, starting from the leftmost-innermost leaves. BottomUp looks like OnceBottomUp but is not similar: s is applied to all nodes, starting from the leaves. Note that the application of s should not fail, otherwise the whole strategy also fails.
The strategy Innermost tries to apply s as many times as possible, starting from the leaves. This construct is useful to compute normal forms.
For example, we define myFirstInnerMost = InnerMost(s) where s is defined as the elementary strategy:
%strategy RewriteSystem() extends Fail() {
visit Term {
a() -> { return `b(); }
b() -> { return `c(); }
g(c(),c()) -> { return `c(); }
}
}
The application of this strategy to different subject terms gives:
| (myFirstInnerMost)[g(a(),b())] | ⇒ | c() |
| (myFirstInnerMost)[f(g(g(a,b),g(a,a)))] | ⇒ | f(c(),c()) |
| (myFirstInnerMost)[g(d(),d())] | ⇒ | g(d(),d()) |
We can notice that Innermost strategy never fails. If we try myFirstBottomUp = BottomUp(s) with the same subjects, we obtain always failure because if s fails on a node, the whole strategy fails.
In order to get more efficient strategies (in particular when performing leftmost-innermost normalization), we consider variants where the notion of failure corresponds to the identity. This means that when a term cannot can be transformed by a strategy (into a different term), this is considered as a failure.
| (SequenceId(s1,s2))[t] | ⇒ | (s2)[t’] if (s1)[t] ⇒t’ with t≠t’ |
| t otherwise | ||
| (ChoiceId(s1,s2))[t] | ⇒ | t’ if (s1)[t] ⇒t’ with t≠t’ |
| (s2)[t] otherwise | ||
| (OneId(s))[f(t1,...,tn)] | ⇒ | f(t1,...,ti’,...,tn) if (s)[ti] ⇒ti’ with ti≠ti’ |
| f(t1,...,tn) otherwise | ||
| (OneId(s))[cst] | ⇒ | cst |
| TryId(s) | = | s |
| RepeatId(s) | = | µ x.SequenceId(s,x)) |
| OnceBottomUpId(s) | = | µ x.ChoiceId(OneId(x),s)) |
| OnceTopDownId(s) | = | µ x.ChoiceId(s,OneId(x))) |
| InnermostId(s) | = | µ x.Sequence(All(x),SequenceId(s,x))) |
| OutermostId(s) | = | µ x.Sequence(SequenceId(s,x),All(x))) |
We can define a strategy trying to apply a simple rewrite system to the root of a term, replacing a() by b(), b() by c(), and g(c(),c()) by a(), and otherwise returning the identity:
import tom.library.sl.*;
We also need to import the corresponding mapping:
%include { sl.tom }
Then we define an elementary strategy:
%strategy RewriteSystem() extends Fail() {
visit Term {
a() -> { return `b(); }
b() -> { return `c(); }
g(c(),c()) -> { return `c(); }
}
}
Then, it becomes quite easy to define various strategies on top of this elementary strategy:
Term subject = `f(g(g(a,b),g(a,a)));
Strategy rule = `RewriteSystem();
try {
System.out.println("subject = " + subject);
System.out.println("onceBottomUp = " +
`OnceBottomUp(rule).visitLight(subject));
System.out.println("innermost = " +
`Choice(BottomUp(rule),Innermost(rule)).visitLight(subject));
} catch (VisitFailure e) {
System.out.println("reduction failed on: " + subject);
}
As mentioned section 11.5, Gom automatically generates congruence and construction strategies for each constructor of the signature.
Strategies can be considered as algebraic terms. For instance, the BottomUp(v) strategy corresponds to the algebraic term mu(MuVar("x"),Sequence(v,All(MuVar("x")))).
Those strategy terms can then be traversed and transformed by mean of strategies. As strategies are considered as algebraic terms, it is possible to use pattern matching on the elementary strategies of the strategy language.
public Strategy topDown2BottomUp(Strategy s) {
%match(s) {
Mu(x,Sequence(v,All(x))) -> {
return `Mu(x,Sequence(All(x),v));
}
}
return s;
}
Strategy expressions being visitable terms, we can also use the ‘%strategy’ construction to define strategy transformations, for example, removing unnecessary Identity() strategies.
%strategy RemId extends Identity() {
visit Strategy {
Sequence(Identity(),x) -> { return `x; }
Sequence(x,Identity()) -> { return `x; }
}
}
The simplest way to use strategies is to apply them on data-structures generated by Gom, as this data structure implementation provides the interfaces and classes needed to use ‘%strategy’. In particular, all the data structure classes implement the tom.library.sl.Visitable interface used as argument of visit methods in the tom.library.sl.Strategy interface. However, it is also possible to use ‘%strategy’ with any term implementation.
We detail here on a simple example of hand written data structure and how to use ‘%strategy’ statements and the Tom strategy library.
Given a Java class Person we can define an algebraic mapping for this class:
%typeterm TomPerson {
implement { Person }
equals(t1,t2) { t1.equals(t2) }
}
For this example, we consider a data-structure those Gom equivalent could be
Term = A()
| B()
| G(arg:Slot)
| F(arg1:Term, arg2:Term)
Slot = Name(name:String)
We first present a very straightforward implementation of this data structure. It will serve as a basis and will be extended to provide support for strategies.
We first define abstract classes for the two sorts of this definition, Term and Slot, and classes for those operators extending those sort classes.
public abstract class Term { }
public abstract class Slot { }
/* A and B are similar up to a renaming */
public class A extends Term {
public String toString() {
return "A()";
}
public boolean equals(Object o) {
if(o instanceof A) {
return true;
}
return false;
}
}
/* G is similar to F, but has only one child */
public class F extends Term {
public Term a;
public Term b;
public F(Term arg0, Term arg1) {
a = arg0;
b = arg1;
}
public String toString() {
return "F("+a.toString()+", "+b.toString()+")";
}
public boolean equals(Object o) {
if(o instanceof F) {
F f = (F) o;
return a.equals(f.a) && b.equals(f.b);
}
return false;
}
}
public class Name extends Slot {
public String name;
public Name(String s) {
this.name = s;
}
public String toString() {
return "Name("+name+")";
}
public boolean equals(Object o) {
if(o instanceof Name) {
Name n = (Name) o;
return name.equals(n.name);
}
return false;
}
}
We only took care in this implementation to get a correct behavior for the equals method. Then, the Tom mapping is simply
%include { string.tom }
%typeterm Term {
implement { Term }
equals(t1,t2) {t1.equals(t2)}
}
%typeterm Slot {
implement { Slot }
equals(t1,t2) {t1.equals(t2)}
}
%op Term A() {
is_fsym(t) { (t!= null) && (t instanceof A) }
make() { new A() }
}
%op Term F(arg1:Term, arg2:Term) {
is_fsym(t) { (t!= null) && (t instanceof F) }
get_slot(arg1,t) { ((F) t).a }
get_slot(arg2,t) { ((F) t).b }
make(t0, t1) { new F(t0, t1) }
}
...
%op Slot Name(name:String) {
is_fsym(t) { (t!= null) && (t instanceof Name) }
get_slot(name,t) { ((Name) t).name }
make(t0) { new Name(t0) }
}
If the classes representing operators do not implement the tom.library.sl.Visitable interface, there is no special code modification for supporting strategies. Users have just to activate the Tom option –gi.
We can use the tom.library.sl.Introspector interface to apply strategies on such terms:
public Object setChildren(Object o, Object[] children); public Object[] getChildren(Object o); public Object setChildAt( Object o, int i, Object child); public Object getChildAt(Object o, int i); public int getChildCount(Object o);
In the tom.library.sl.Strategy interface, there exist corresponding methods to visit objects that do not implement the tom.library.sl.Visitable interface:
public Object visit(Object any, Introspector i) throws VisitFailure; public Object visitLight(Object any, Introspector i) throws VisitFailure; public Object visit(Environment envt, Introspector i) throws VisitFailure;
In the implementation of these methods, the introspector behaves like a proxy to render any object visitable. When activating the Tom option –gi, the compiler generates in each Tom class an inner class named LocalIntrospector that implements the tom.library.sl.Introspector interface. This class uses informations from the mappings to know how visiting the corresponding classes.
For example, we can define the following ‘%strategy’ statement:
%strategy Rename(oldname:String,newname:String) extends Identity() {
visit Slot {
Name(n) -> {
if(n.equals(oldname)) {
return `Name(newname);
}
}
}
}
Then by using the generated class LocalIntrospector, it is possible to use the strategy Rename with any strategy combinators:
public static void main(String[] args) {
Term t = `F(F(G("x"),G("y")),G("x"));
`TopDown(Rename("x","z")).visit(t, new LocalIntrospector());
}
The system comes with several predefined signature-mappings for C, Java and Caml. Among them, let us mention:
These mappings define, for each builtin sort of the host language, an algebraic sort that can be used in a %match or a signature definition construct. Thus, builtin values, such as f(5), g(’a’) or h("foo"), can be used in patterns.
The string.tom mapping is interesting because it provides an associative operator (concString) which allows the programmer to consider a string as a list of characters. Thus, the string "foo" can be seen as the algebraic object concString(’f’,’o’,’o’). By using this mapping, it becomes possible to perform pattern matching against the content of a string. The pattern concString(’f’,X*) will match any string which begins with the character ’f’. By using the unnamed-symbol capability, this pattern can be written: (’f’,X*) instead of concString(’f’,X*).
To match any string which begins with the substring "fo", the corresponding pattern should be (’f’,’o’,X*). To simplify the definitions of such patterns, Tom supports an exception which allows the programmer to write (’fo’,X*) instead. Internally, the ill-formed character ’fo’ is expanded into the list (’f’,’o’).
In addition to these mappings, several other predefined mappings come with the system:
To help manipulating Java data-structures, Tom provides several mappings for the Java Runtime Library. The naming convention follows Java’s one:
java
o--- Character.tom
+--- util
o--- ArrayList.tom
o--- HashMap.tom
o--- HashSet.tom
o--- LinkedList.tom
o--- MapEntry.tom
o--- TreeMap.tom
o--- TreeSet.tom
+--- types
o--- AbsractCollection.tom
o--- AbsractList.tom
o--- AbsractSequentialList.tom
o--- AbsractSet.tom
o--- ArrayList.tom
o--- Collection.tom
o--- HashMap.tom
o--- HashSet.tom
o--- LinkedHashSet.tom
o--- Map.tom
o--- Object.tom
o--- Stack.tom
o--- TreeMap.tom
o--- TreeSet.tom
o--- Vector.tom
o--- WeakHashMap.tom
The directory types contains only %typeterm declarations.
To support strategies, Tom provides a runtime library, called SL and implemented in strategy.jar. This library implements the elementary strategy combinators (Identity, Fail, All, One, Choice, Sequence, etc.) as well as basic support for the computation of positions described in section 12.1.2.
In addition, some predefined mapping are also available to allow the description of strategies:
The class tom.library.utils.Viewer contains a set of methods to visualize visitable terms.
/* dot representations */ // on the writer stream public static void toDot(tom.library.sl.Visitable v, Writer w) // on the standard output stream public static void toDot(tom.library.sl.Visitable v) /* pstree-like representations */ // on the writer stream public static void toTree(tom.library.sl.Visitable v, Writer w) // on standard output stream public static void toTree(tom.library.sl.Visitable v) /* gui display */ public static void display(tom.library.sl.Visitable v)
Note that these methods can also be used on strategies as they are also visitable.
To support the transformation of Xml documents, Tom provides a specific syntax for defining patterns, as well as several predefined mappings:
See Section 10.4 for a detailed description of the Xml facilities offered by Tom.
To manipulate Java classes, Tom provides a library which supplies a Gom term usable by Tom out of a Java class. The library enables to define transformations of this term by strategic rewriting as well as functionalities to generate a new Java class from the modified term.
This approach is similar to BCEL library in the sense that we construct a complete representation of the class. But thanks to Gom, we obtain a very efficient structure with maximal sharing. Moreover, thanks to associative matching, we can easily express patterns on the bytecode and in this way, ease the definition of transformations.
The library generates a Gom term using the ASM library. This term is a memory-efficient representation of the Java class, which can then be traversed and transformed using Tom. After translating the Java class into a Gom term, we use Tom features to define transformations and traversals and to obtain a new Gom term which can be transformed into a new Java class.
To support the analysis and transformation of Java bytecode programs, Tom provides several mappings:
In order to represent bytecode programs, we have defined a Gom signature that allows us to represent any bytecode program by a typed term. Given a Java class, we use ASM to read the content and build an algebraic representation of the complete Java class. This approach is similar to BCEL. Contrary to ASM, this permits multi-pass or global analysis.
module Bytecode
imports int long float double String
abstract syntax
TClass = Class(info:TClassInfo, fields:TFieldList,
methods:TMethodList)
...
TMethodList = MethodList(TMethod*)
TMethod = Method(info:TMethodInfo, code:TMethodCode)
TMethodCode = MethodCode(instructions:TInstructionList,
localVariables:TLocalVariableList,
tryCatchBlocks:TTryCatchBlockList)
...
TInstructionList = InstructionList(TInstruction*)
TInstruction = Nop()
| Iload(var:int)
| Ifeq(label:TLabel)
| Invokevirtual(owner:String, name:String,
methodDesc:TMethodDescriptor)
...
The real signature (adt/bytecode/Bytecode.tom) contains more than 250 different constructors. The given signature shows that a class is represented by a constructor Class, which contains information such as name, packages, and imports. It also contains a list of fields and a list of methods. The latter is encoded using an associative operator MethodList. Similarly, a list of instructions is represented by the associative operator InstructionList. A method contains an info part and a code part. The code part is mainly composed by local variables and a list of instructions. Each bytecode instruction is represented by an algebraic constructor: Nop, Iload, etc.
In the package tom.library.bytecode, there exist two principal classes based on the ASM library:
public static byte[] transform(String file){
BytecodeReader br = new BytecodeReader(file);
TClass c = br.getTClass();
TClass cc = transform(c);
BytecodeGenerator bg = new BytecodeGenerator();
return bg.toBytecode(cc);
}
When considering a Bytecode program, with the sl library, we can just define traversals without considering the control flow. Our suggestion is to use strategies in order to simulate the control flow during the traversal of the list of instructions. In the Tom language, the rules and the control are completely separated so an alternative for representing control flow graphs (CFG) is to use the control to indicate what is the possible following instruction. We have seen in the previous section that to apply a strategy to children, there exist two combinators All and One.
In the mapping bytecode/cfg.tom, the two combinators AllCfg and OneCfg behave almost as All and One but the considered children are the following instructions in the Control flow graph instead of the following instruction in the list. For example, the Goto instruction has one child with respect to the control flow graph (the instruction corresponding to the label). An If_XX instruction has two children: the one which satisfies the expression, and the one that does not.
Part IV |
This chapter describes how to install and use the Tom system.
Tom is a Java application written with JDK 1.5. Tom is platform independent and runs on various systems. It has been used successfully on many platforms, including Linux (Debian, Mandrake, Ubuntu), FreeBSD, NetBSD, MacOS X, and Windows XP.
The only requirement to run Tom is to have a recent Java Runtime Environment installed (version 1.5 or newer) and/or the Eclipse platform (3.2 or newer). In addition, Ant can be useful to compile the system and the examples:
The binary distribution of Tom consists of the following directory layout:
tom
+--- bin // contains launcher scripts
+--- lib // contains Tom jars and necessary dependencies
| +--- runtime (BSD Licence)
| +--- tom (GPL Licence)
| +--- tools
|
+--- share
+--- contrib
+--- man
+--- tom // contains predefined mapping
+--- adt
+--- c
+--- caml
+--- java
To install Tom, choose a directory and copy the distribution files there. This directory will be designed in the following by TOM_HOME.
JDK 1.5 or newer is required.
For a painless process, please use the install kit provided. This will automatically update the environment as needed.
Anyway, if for any reason you want to do it all manually, here is the procedure you need to follow:
We assume that Tom is installed in c:\tom. The following steps are needed for setting up the environment:
For a detailed description of setting environment variables in
Windows, please refer to Windows documentation. For Windows XP, some
information can be found here:
http://support.microsoft.com/default.aspx?scid=kb;en-us;310519&sd=tech
If you installed Tom using the install kit, the installation is complete. If you want to install it manually (not recommended), please use the following instructions.
We assume that Tom is installed in c:\tom\. Please issue the following for setting up Tom:
export TOM_HOME=/cygdrive/c/tom
export PATH=${PATH}:${TOM_HOME}/bin
We also suggest you to define a TOM_LIB variable and update your CLASSPATH accordingly:
for i in "${TOM_HOME}"/lib/runtime/*.jar
do
TOM_LIB="$TOM_LIB:$i"
done
export CLASSPATH=${TOM_LIB}:${CLASSPATH}
Assuming Tom is installed in /usr/local/tom. The following sets up the environment:
(bash)
export TOM_HOME=/usr/local/tom
export PATH=${PATH}:${TOM_HOME}/bin
(csh)
setenv TOM_HOME /usr/local/tom
set path=( $path ${TOM_HOME}/bin )
We also suggest you to define a TOM_LIB variable and update your CLASSPATH accordingly:
(bash)
for i in "${TOM_HOME}"/lib/runtime/*.jar
do
TOM_LIB="$TOM_LIB:$i"
done
export CLASSPATH=${TOM_LIB}:${CLASSPATH}
(csh)
set TOM_LIB=`echo ${TOM_HOME}/lib/runtime/*.jar | tr ' ' ':'`
setenv CLASSPATH ${TOM_LIB}:${CLASSPATH}
The Tom eclipse plugin is available directly from the Eclipse
platform via the update link:
http://tom.loria.fr/plugin.php
From the Help menu, choose Help Content and look at the Tom Section. You will find there everything to use Tom in a very simple way.
Many examples have been written to test or illustrate some particular behaviors. This collection of examples is available at the http://tom.loria.fr/download.php page.
The Tom and Gom compilers are written in Tom itself. The compiler is certainly the most complex program written in Tom. Most of the constructs provided by Tom are used and tested in the project itself.
The Tom and Gom sources are available through anonymous cvs(1). To get them, use the commands:
cvs -d :pserver:anonymous@scm.gforge.inria.fr:/cvsroot/tom login cvs -d :pserver:anonymous@scm.gforge.inria.fr:/cvsroot/tom checkout -P jtom
Developer access is possible via ssh. See Gforge for detailed instructions.
The cvs checkout will get a new repertory in your current working directory, called jtom. We will call this directory ${TOM_BASE}.
First of all, please read ${TOM_BASE}/INSTALL. Even if the current guide should be enough, this file may contain useful information.
The Tom build process uses apache ant to automate the all parts of the process. This build process is specified by the ${TOM_BASE}/build.xml file. You will need to install apache ant and Java 1.5 in order to compile Tom.
The build process requires apache ant 1.7 or more, and a Java environment compatible with Java 1.5.
Optionally, to customize the build environment, you will have to copy the template configuration file ${TOM_BASE}/local.properties_template to ${TOM_BASE}/local.properties, and edit the latter it to reflect your setup. The most common is to set build.compiler=jikes to use the jikes Java compiler, and build.compiler.emacs=true to get errors in a format the emacs editor can handle.
To compile the stable distribution of Tom, you have to use the ${TOM_BASE}/build.sh script. To use it, first make sure to cd(1) to ${TOM_BASE}. Then you can build the stable distribution.
$ ./build.sh stable
This creates the stable distribution in the directory ${TOM_BASE}/stable/dist.
To build and install the source distribution, you have to do the following:
$ ./build.sh stable $ ./build.sh src.dist
This creates the src distribution in the directory ${TOM_BASE}/src/dist.
To list all the available targets for the build:
$ ./build.sh -projecthelp
To setup Tom after a source build, you can simply follow the configuration instructions for the binary distribution found in Section 14, using either ${TOM_BASE}/stable/dist or ${TOM_BASE}/src/dist for value for the TOM_HOME environment variable.
The Tom compiler is a non-intrusive pattern matching compiler. It takes a Tom program, combination of a host programming language (Java, C or Caml) extended by Tom constructs. Each Tom program can define its own data structures and manipulate them in order to write pattern-matching based algorithms.
As mentioned earlier, Tom generates host language code. The command tom invokes the compiler on a Tom source file and generates a new source file (with .java, .tom.c, or .tom.ml extension, depending on the compilation command-line). The generated code has to be compiled/interpreted by a tool which can handle the corresponding host language: javac for Java, cc for C and ocamlc for Caml.
A typical development cycle is the following:
As cc and javac, tom can compile several input files. By default, the generated files are saved in the same directory as the corresponding input files. When compiling a Java file (i.e. a Tom file where Java is the host language), Tom is smart enough to parse the package definition and generate the pure-Java file in the same package architecture. Similarly to javac, tom supports a -d option which allows the user to indicate where the files have to be generated. To be compatible with cc and classical Makefile, Tom also supports a -o option which can be used to specify the name of the generated file.
tom [options] filename[.t]
The command takes only one file argument, the name of the input file to be compiled. By convention the input file name is expected to be of the form filename.t, whatever the used host language is.
Options:
--config | -X <file>Define an alternate XML configuration file Allow to define the plugins instantiated by the Tom platform --cCode | -cGenerate C code (default is Java) The output file has the extension .tom.c --camlCodeGenerate Caml code (default is Java) --camlSemanticsVerify with caml semantics for match) --compileActivate the compiler (by default) --csCodeGenerate C# code --destdir | -dSpecify where to place generated files. By default, Tom generates files close to the input file. However (like javac), this option allows to specify a directory where generated files have to be put. When compiling a Java file, Tom is smart enough to parse the package definition and generate the pure-Java file in the same package architecture. --eclipseActivate Eclipse mode --encoding <charset> | -eSpecify the character encoding --expandActivate the expander (by default) --genIntrospector | -giGenerate a class that implements Introspector to apply strategies on non visitable terms --help | -hShow the help Give a brief description of each available options --import <path> | -IPath to included files Even if inclusion can be performed using relative path, this option specifies list of path where Tom look for when an inclusion has to be done by %include construct --inlineInline mapping --inlineplusForce inlining, even if no $is used--intermediate | -iGenerate intermediate files The compiler manipulates Abstract Syntax Trees. This option dumps the AST after each phase (parsing, checking, expansion, compilation) This option is useful to analyze the compilation process --jCode | -jGenerate Java code (by default) --lazyType | -lUse universal type This option makes Tom using a less restrictive backend. In Java, the universal sort Object is used more often. This reduces static typing but allows to manipulate inherited data-structures --noDeclaration | -DDo not generate code for declarations Avoid multiple declaration of symbols when structures are inherited or when multiple inclusion of common data structures are performed --noOutputDo not generate code No output file is generated. It allows to see warnings and errors without generating the result --noReduceDo not simplify extracted constraints (depends on –verify) --noStaticGenerate non static functions --noSyntaxCheckDo not perform syntax checking --noTypeCheckDo not perform type checking --optimize | -OOptimize generated code Add an optimization phase to the compilation process. This removes unused variables and performs some inlining. --optimize2 | -O2Further optimize generated code (does not imply -O)--output | -oSet output file name By default, Tom infers the name of the generated file by replacing the initial file extension by .java, .tom.c or .tom.ml, depending on the chosen target language. This option allows to explicitly give the name of the generated file. --pCodeGenerate Python code --parseActivate the parser (by default) --pretty | -pGenerate readable code with indentation By default, the generated code is synchronized with the source code. This simplifies error reporting but makes the code more difficult to read. This option beautifies the generated code. --prettyPIL | -pilPrettyprint the intermediate language --protectedGenerate protected functions In Java, this option forces the generation of protected functions, instead of private ones, for symbol manipulation functions --typeTyper (activated by default) --verbose | -vSet verbose mode on Give duration information about each compilation passes --verifyVerify correctness of match compilation --version | -VPrint the version of Tom --wallPrint all warnings Useful in debugging phase
Tom provides an ant task for running the Tom compiler within the apache ant build system.
The Tom ant task is very close in use to the javac ant task. Since this task is not part of the official ant tasks, you have first to declare this task in your buildfile, in order to use it.
This is done by the following code:
<taskdef name="tom" classname="tom.engine.tools.ant.TomTask"> <classpath refid="tom.classpath"/> </taskdef>
where tom.classpath is the path reference containing all the jar’s
in Tom’s distribution predefined in the file ${TOM_HOME}/lib/tom-common.xml.
This task is used to produce Java code from Tom programs. A typical use of the Tom ant task is:
<tom config="${tom.configfile}"
srcdir="${src.dir}"
destdir="${gen.dir}"
options="-I ${mapping.dir}">
<include name="**/*.t"/>
</tom>
Here, we want to compile all Tom source files in {src.dir},
having the generated code in {gen.dir}, and we configure the compiler
to use the {tom.configfile} config file, and pass the options we
want like, for example {-I} to indicate the mapping needed for compilation, just as we do for Tom in command line.
Another use of this task is:
<tom config="${tom.configfile}"
srcdir="${src.dir}"
outputfile="${gen.dir}/Example.java"
options="-I ${mapping.dir}">
<include name="**/Example.t"/>
</tom>
Here we compile only one Tom file, and specify directly the output file name we want to use.
The main usecases for the Tom ant task can be found in Tom’s own buildfile.
The Tom ant task takes the following arguments:
| Attribute | Description | Required |
| classpath | The classpath to use, given as a reference to a path defined elsewhere. This variable is not used currently. | No |
| config | Location of the Tom configuration file. | No |
| destdir | Location of the Java files. | No |
| failonerror | Indicates whether the build will continue even if there
are compilation errors; defaults to true | No |
| logfile | Which log file to use. | No |
| nowarn | Asks the compiler not to report all warnings; defaults to
no | No |
| optimize | Indicates whether source should be compiled with
optimization; defaults to off | No |
| options | Custom options to pass to the Tom compiler | No |
| outputfile | Destination file to compile the source. This require to have only one source file. | No |
| pretty | Asks the compiler to generate more human readable code;
defaults to no | No |
| srcdir | Location of the Tom files. | Yes, unless nested
<src> elements are present |
| verbose | Asks the compiler for verbose output; defaults to
no | No |
People interested in using Gom as a standalone tool can use the Gom command line interface.
gom [options] filename [... filename]
Options:
--config <file> | -X | Defines an alternate XML configuration file |
--debug | -vv | Display debugging info |
--destdir <dir> | -d | Specify where to place generated files |
--generator <type> | -g | Select Generator. Possible value: "shared" |
--help | -h | Show this help |
--import <path> | -I | Path for include |
--inlineplus | Make inlining active |
--intermediate | -i | Generate intermediate files |
--intermediateName <intermediateName> | -iname | specify the prefix of intermediate files |
--multithread | -mt | Generate code compatible with multi-threading |
--optimize | -O | Optimize generated code |
--optimize2 | -O2 | Optimize generated code |
--package <packageName> | -p | Specify package name (optional) |
--strategies-mapping | -sm | Generate tom mapping for strategies |
--termgraph | -tg | Extend the signature for term-graphs |
--termpointer | -tp | Extend the signature for term pointers |
--verbose | -v | Display compilation information |
--verbosedebug | -vvv | Display even more debugging info |
--version | -V | Print version |
--wall | -W | Print warning |
Gom can also be used within ant, and has its own ant tasks.
To use the Gom ant task, you have to first declare it the same way as the Tom ant task.
<taskdef name="gom"
classname="tom.gom.tools.ant.GomTask"
classpathref="tom.classpath"/>
Once the task is defined, you can use them to compile a Gom file.
The Gom ant task has to be able to find a configuration file for Gom.
It can either use the tom.home property to find its configuration file,
or use the value of the config attribute.
Since the tom.home property is also used when Gom has to process
hooks, it is a good practice to always define the tom.home property to
the installation path of the Tom system.
The default configuration file for
Gom is included in the Tom distribution as Gom.xml.
<gom config="${gom.configfile}"
srcdir="${src.dir}"
package="example"
destdir="${gen.dir}">
<include name="**/*.gom"/>
</gom>
Like in Tom example, in this Gom ant task we want to compile all Gom source files in {src.dir} and to configure the compiler to create a package called example in {gen.dir} for the generated code, just as we do for Gom in command line.
The Gom task takes the following arguments:
| Attribute | Description | Required |
| config | Location of the Gom configuration file. | No |
| destdir | Location of the generated files. | No |
| options | Custom options to pass to the Gom compiler. | No |
| package | Package for the generated Java files. | No |
| srcdir | Location of the Gom files | Yes, unless nested
<src> elements are present |
The set of .gom files to compile is specified with a nested
include element.
GomAntlrAdaptor is a tool that takes a Gom signature and generates an adaptor for a given Antlr grammar file. This way, Gom constructors can be directly used in the rewrite rule mechanism offered by Antlr (version 3). See examples/parser the see an example that shows how to combine Tom, Gom and Antlr.
gomantlradaptor [options] filename [... filename]
Options:
--config <file> | -X | Defines an alternate XML configuration file |
--debug | -vv | Display debugging info |
--destdir <dir> | -d | Specify where to place generated files |
--grammar <grammarName> | -g | Antlr grammar name |
--help | -h | Show this help |
--import <path> | -I | Path for include |
--intermediate | -i | Generate intermediate files |
--intermediateName <intermediateName> | -iname | specify the prefix of intermediate files |
--package <packageName> | -p | Specify package name (optional) |
--termgraph | -tg | Extend the signature for term-graphs |
--termpointer | -tp | Extend the signature for term pointers |
--verbose | -v | Display compilation information |
--verbosedebug | -vvv | Display even more debugging info |
--version | -V | Print version |
--wall | -W | Print warning |
The GomAntlrAdaptor task takes the following arguments:
| Attribute | Description | Required |
| config | Location of the GomAntlrAdaptor configuration file. | No |
| destdir | Location of the generated files. | No |
| grammar | Name of the grammar. | Yes |
| options | Custom options to pass to the Gom compiler. | No |
| package | Package for the generated Java files. | No |
| srcdir | Location of the GomAntlrAdaptor files | Yes, unless nested
<src> elements are present |
The Tom distribution contains some filetype plugins for Tom and Gom support in Vim. They are located in ${TOM_HOME}/share/contrib/vim.
To install them, you should put the content of the contrib/vim directory in ${HOME}/.vim/. Then in order for these plugins to be automatically used whenever it is necessary, you can put in your ${HOME}/.vimrc:
" indentation depends on the filetype filetype indent on filetype plugin on
Also, to have vim automatically loading Tom and Gom plugins when editing Tom and Gom files, you can edit (or create) the file ${HOME}/.vim/filetype.vim:
if exists("did_load_filetypes")
finish
endif
augroup filetypedetect
au! BufNewFile,BufRead *.t setfiletype tom
au! BufNewFile,BufRead *.tom setfiletype tom
au! BufNewFile,BufRead *.gom setfiletype gom
augroup END
For Tom developers, the preferred setup for indenting Tom and Java code is as follows, to be placed in ${HOME}/.vimrc:
autocmd FileType ant set expandtab autocmd FileType ant set sw=2 " automatically indent tom and java code autocmd FileType java,tom,gom set cindent autoindent autocmd FileType java,tom,gom set encoding=utf-8 autocmd FileType java,tom,gom set fileencoding=utf-8 " how to indent: in java and tom, 2 spaces, no tabs autocmd FileType java,tom,gom set expandtab autocmd FileType java,tom,gom set sw=2 autocmd FileType java,tom,gom set tabstop=2 autocmd FileType java,tom,gom set nosmarttab
To compile Tom programs (like Tom) under Vim, and get a correct error reporting, you will have to set the ${CLASSPATH} environment value to the path of junit.jar, and use the makeprg variable to have :make call ant through a script maintaining the link between Tom and the generated Java files. We suppose here that Tom was installed in ${HOME}, i.e. ${TOM_HOME} is ${HOME}/workspace/jtom.
let $CLASSPATH = "${HOME}/workspace/jtom/src/lib/tools/junit.jar"
set makeprg=ant\ -find\ build.xml\ -emacs\ $*\\\|\
\ awk\ -f\ \"${HOME}/workspace/jtom/utils/ant-tom.awk\"
Zsh completion functions for Tom and Gom are available in the share/contrib/zsh directory. To install them, you only have to add those files to zsh’s fpath variable.
For example, assuming you already set up the ${TOM_HOME} environment variable to the Tom installation directory, you can add to your ${HOME}/.zshrc:
fpath=(${TOM_HOME} $fpath)
To build complex projects using Tom, it is useful to use Ant as build system, to manage generation of data structure using Gom and the compilation of Tom and Java code.
To ease the use of Ant, the file ${TOM_HOME}/lib/tom-common.xml is provided in the Tom distribution. This file provide initialization for Tom and Gom Ant tasks. To load tom-common.xml, you just have to put in your Ant script:
<property environment="env"/>
<property name="tom.home" value="${env.TOM_HOME}"/>
<import file="${tom.home}/lib/tom-common.xml"/>
Then, each target depending on the tom.init task will allow the use of the Gom and Tom ant tasks, as well as tom.preset and javac.preset, providing usual values for the attributes of those tasks. Also, tom-common.xml provides several properties, as tomconfigfile and gomconfigfile, providing the location of the configuration files for Tom and Gom, and tom.classpath, containing all classes related to the Tom installation.
For example, if you have a directory called tom_example with Tom source files and Gom source files which generate the Tom mapping required by tom_example, you can create the following Ant script to compile all Gom, Tom and Java code.:
<?xml version="1.0" encoding="ISO-8859-1"?>
<project name="Example Ant for TOM" basedir="." default="compile">
<description>
A simple example of build script using Ant offering compilation of TOM programs.
</description>
<!-- Initializing Tom and Gom -->
<property environment="env"/>
<property name="tom.home" value="${env.TOM_HOME}"/>
<import file="${tom.home}/lib/tom-common.xml"/>
<!-- Defining folders -->
<property name="my_example" value="tom_example"/>
<property name="src.dir" value="."/>
<property name="gen.dir" value="gen"/>
<property name="build.dir" value="build"/>
<property name="mapping.dir" value="${gen.dir}/${my_example}/${my_example}"/>
<!-- Declaring Tom task -->
<taskdef name="tom" classname="tom.engine.tools.ant.TomTask">
<classpath refid="tom.classpath"/>
</taskdef>
<!-- Declaring Gom task -->
<taskdef name="gom"
classname="tom.gom.tools.ant.GomTask"
classpathref="tom.classpath"/>
<target name="init" depends="tom.init" description="To realize initialization">
<mkdir dir="${gen.dir}"/>
<mkdir dir="${build.dir}"/>
</target>
<target name="compile" depends="init" description="To compile all programs">
<!-- Compiling Gom programs -->
<gom config="${gomconfigfile}"
srcdir="${src.dir}"
package="${my_example}"
destdir="${gen.dir}">
<include name="**/*.gom"/>
</gom>
<!-- Compiling Tom programs -->
<tom config="${tomconfigfile}"
srcdir="${src.dir}"
destdir="${gen.dir}"
options="-I ${mapping.dir}">
<include name="**/*.t"/>
</tom>
<!-- Compiling Java programs -->
<javac srcdir="${gen.dir}" destdir="${build.dir}">
<classpath path="${build.dir}"/>
<include name="**/*.java"/>
</javac>
</target>
<target name="clean" description="To remove generated code">
<delete dir="${gen.dir}"/>
<delete dir="${build.dir}"/>
</target>
</project>
This chapter documents important changes in the Tom language that impact running code. We explain how to modify your programs in order to be able to use the last version of Tom.
Representation of lists (FL). The default behaviour of lists is FL. The semantics has changed in case of associative symbol under an other associative symbol.
Gom syntax. The syntax compatibility with Vas is now not available.
The %rule has been removed. It can be replaced by rules hooks in
Gom, described in Section 11.2. The syntax for rules is
unchanged, except that ‘where’ clauses are no more supported.
Since rules are integrated into the code generated by Gom, it is no more
possible to short-circuit rule application by calling Java functions
instead of ‘‘’ to built terms.
%include { mustrategy.tom } should be replace by %include { sl.tom }
Any reference to jjtraveler or tom.library.strategy.mutraveler should be replaced by a reference to tom.library.sl:
import tom.library.strategy.mutraveler.*; by import tom.library.sl.*;
import jjtraveler.*; by import tom.library.sl.*;
jjtraveler.Visitable by tom.library.sl.Visitable
jjtraveler.VisitFailure by tom.library.sl.VisitFailure
jjtraveler.Visitor by tom.library.sl.Strategy
jjtraveler.reflective.VisitableVisitor by tom.library.sl.Strategy
MuStrategy by Strategy
getPosition() should be replaced by getEnvironment().getPosition()
apply(...) should be replaced by visit(...) or visitLight(...), enclosed by a try ... catch(VisitFailure e) ...
Call to MuTraveler.init should be removed
The backquote for the default strategy in %strategy could be removed.
Since version 2.4, builtin sorts (int, long, String, etc.) are no longer implicit. The corresponding %include { ... } must be done explicitly.
Since version 2.4, ApiGen and Vas are obsolete. Gom should be used instead.
To avoid ambiguities, since version 2.3, constants should be written using explicit parentheses: a(), nil(), for example. To be coherent, the parentheses have also to be used in the mapping definition:
%op T a() {
...
}
Since version 2.3, Tom generate static functions in Java, instead of object methods. This allows to use Tom constructs in the main() function, this improves the efficiency of the generated code, and this makes safer the use of strategies.
To be compatible with the previous version, the –noStatic flag can be used.
In the future, Gom will replace Vas. To make the migration easier, the Gom compiler accepts the Vas syntax. However, there are some minor changes:
Since version 2.2, the mapping definition formalism has been simplified. Therefore, we are no longer able to be fully compatible with the old syntax. Some small and simple modifications have to be performed:
%op T f(T,T) has to be replaced by %op T f(arg1:T,arg2:T), where arg1 and arg2 are slot-names.
The definition of get_slot can be defined by using the previously defined construct get_subterm (the first slot corresponds to the 0−th subterm, second slot to the 1−st subterm, etc.). Thus, for the previous example, we can have:
%op T f(arg1:T, arg2:T) {
get_slot(arg1,t) { get_subterm(t,0) }
get_slot(arg2,t) { get_subterm(t,1) }
}
%op T f(arg1:T, arg2:T) {
is_fsym(t) { cmp_fun_sym(get_fun_sym(t), body of the old fsym construct) }
get_slot(arg1,t) { get_subterm(t,0) }
get_slot(arg2,t) { get_subterm(t,1) }
}
As an example, let us consider the following “old” mapping definition:
%typeterm TomTerm {
implement { ATermAppl }
cmp_fun_sym(t1,t2) { t1 == t2 }
get_fun_sym(t) { t.getName() }
get_subterm(t, n) { t.getArgument(n) }
equals(t1, t2) { t1 == t2 }
}
%typelist TomList {
implement { ATermList }
get_fun_sym(t) { ((t instanceof ATermList)?"conc":null) }
cmp_fun_sym(t1,t2) { t1 == t2 }
equals(l1,l2) { l1 == l2 }
get_head(l) { (ATermAppl)l.getFirst() }
get_tail(l) { l.getNext() }
is_empty(l) { l.isEmpty() }
}
%op TomTerm a {
fsym { "a" }
make() { factory.makeAppl(factory.makeAFun("a", 0, false)) }
}
%op TomTerm f(TomTerm) {
fsym { "f" }
make(t1) { factory.makeAppl(factory.makeAFun("f", 1, false),t1) }
}
%oplist TomList conc( TomTerm* ) {
fsym { "conc" }
make_empty() { factory.makeList() }
make_insert(e,l) { l.insert(e) }
}
The two first type definitions have to be replaced by:
%typeterm TomTerm {
implement { ATermAppl }
equals(t1, t2) { t1 == t2 }
}
%typeterm TomList {
implement { ATermList }
equals(l1,l2) { l1 == l2 }
}
The operator definition can be replaced by the following code:
%op TomTerm a {
is_fsym(t) { t.getName() == "a" }
make() { factory.makeAppl(factory.makeAFun("a", 0, false)) }
}
%op TomTerm f(arg:TomTerm) {
is_fsym(t) { t.getName() == "f" }
get_slot(arg,t) { (TomTerm) t.getArgument(t,0) }
make(t1) { factory.makeAppl(factory.makeAFun("f", 1, false),t1) }
}
%oplist TomList conc( TomTerm* ) {
is_fsym(t) { t instanceof ATermList }
get_head(l) { (ATermAppl)l.getFirst() }
get_tail(l) { l.getNext() }
is_empty(l) { l.isEmpty() }
make_empty() { factory.makeList() }
make_insert(e,l) { l.insert(e) }
}
Since version 2.2, the disjunction of patterns construct has become deprecated. It can still be used, but we recommend to use the disjunction of symbols instead. This last construct allows to share patterns which have similar subterms but different head-symbols. Therefore, the construct g(g(a)) ∣ g(h(a)) can be replaced by g( (g ∣ h)(a) ). Since version 2.2, this construct has been extended to support disjunction of symbols which do not have identical signature: only involved slots have to be compatible.
Considering %op T f(arg1:T, arg2:T) and %op T g(arg1:T), it is now possible to write g( (g ∣ f)[arg1=a] ).
To prepare a future extension where variables have to be distinguished from constructors of arity 0, we have turned into error all ambiguities between variables and constructors. As a consequence, a variable cannot any longer have the same name as a constant.
Since version 2.2, ApiGen and Vas have been updated:
The TravelerFactory class has been removed and replaced by a Tom mapping: mutraveler.tom. Therefore, backquote notation has to be used: travelerFactory.Repeat(travelerFactory.OnceBottomUp(rule)) is replaced by ‘Repeat(OnceBottomUp(rule)).
Since version 2.1, the runtime library has been reorganized. Java importations have to be updated according to the following hierarchy:
tom
|--- library
| |--- adt (datatype definitions)
| |--- mapping (predefined mapping)
| |--- adt (generated mapping)
| |--- plugin (platform tools)
| |--- set (to handle sets)
| |--- strategy
| |--- concurrent (to support parallel strategy)
| |--- traversal (generic traversal)
| |--- xml (xml tools)
|
|--- platform (the Tom Plugin Platform, known as Tom server)
|--- adt
Since version 2.0, Tom integrates an optimizer which removes unused variable assignments and performs inlining optimizations. In order to make these optimizations correct, the Tom compiler needs to know whether a Tom variable (instantiated by pattern matching) is used or not.
In previous versions of Tom, it was possible to use or re-assign a Tom variable without any particular requirement. Since version 2.0, it is recommended (and needed if you want to use the optimizer) to use the backquote mechanism to retrieve the value of a Tom variable. The syntax of a backquote construct has been modified in the following way:
Since version 2.0, Tom does no longer support predefined builtin sorts, via %typeint, %typestring or %typedouble. Tom comes now with a library of predefined mappings. Among them, int.tom, string.tom and double.tom. In order to use these mappings, the %include construct should be used (i.e. %include{ int.tom } to import the predefined int mapping).
This document was translated from LATEX by HEVEA.